Q - Uma distribuição esférica de carga de raio possui densidade dada por em que é uma constante positiva dada por .
Calcule o campo elétrico produzido em um ponto arbitrário dentro e em um ponto arbitrário fora da distribuição. Deixe o resultado em termos de .
Qual é o valor de para o qual o campo é máximo? Qual é o valor do campo máximo?
Faça um gráfico de vs para todo .
Passo 1
Vem comigo que a gente resolve essa questão juntos!
Essencialmente precisamos achar o campo dentre da distribuição de cargas e o campo fora da distribuição de cargas. Para isso vamos usar a lei de Gauss ao nosso favor, dada por:
Onde é a superfície Gaussiana que vamos utilizar para envolver a região que vamos analisar e é a carga envolvida por essa superfície.
Tendo esses campos poderemos encontrar o campo máximo e desenhar o gráfico do campo vs .
Passo 2
Vamos considerar uma esfera gaussiana com raio , vamos aplicar a lei de Gauss para essa superfície, temos:
Onde é a carga dentro dessa superfície que traçamos. Mas como descobrir quanto vale essa carga?
Bem, o enunciado nos deu a densidade de cargas, usando que:
Onde , já que a densidade só varia na direção radial.
Então, vamos integrar dos dois lados onde a integral em vai de a , assim:
Passo 3
Voltando a lei de Gauss temos:
Agora olhando a integral do lado esquerdo, podemos colocar para fora dela já que não tem motivo para esse campo não ser homogêneo ao longo da superfície, já que ele é radial. Então:
A integral de nos fornece a área da superfície gaussiana que consideremos, assim:
Passo 4
Agora vamos achar o campo fora da distribuição de carga. Vamos de novo considerar uma superfície Gaussiana com um raio , vamos aplicar a lei de Gauss para essa superfície, temos:
Onde dessa vez é a carga total que temos na distribuição de cargas. Para achar essa carga total, vamos fazer a mesma coisa que fizemos para achar a carga interna a superfície de raio , só que agora o limite de integração vai de a , assim temos:
Assim temos:
Passo 5
Voltando a lei de Gauss temos:
Agora olhando a integral do lado esquerdo, podemos colocar para fora dela já que não tem motivo para esse campo não ser homogêneo ao longo da superfície, já que ele é radial. Então:
A integral de nos fornece a área da superfície gaussiana que consideremos, assim:
Passo 6
Agora vamos encontrar o valor de que faz o campo ser máximo e também o valor desse campo máximo.
Sabemos o seguinte sobre o campo .
Para :
Para , temos:
Vemos que o campo máximo vai ocorrer dentro da distribuição de cargas ele cresce com a distância e depois começa a cair já que é uma função quadrada.
Assim o campo máximo vai ocorrer quando:
Assim:
Essa é a posição onde temos o campo máximo, e seu valor é dado por:
Passo 7
O gráfico do campo elétrico fica da seguinte forma:
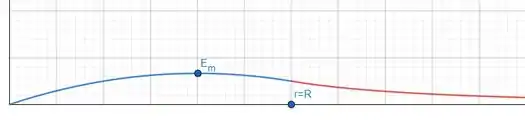
Resposta
Para :
Para , temos: