Um bloco de massa colide com velocidade com um pêndulo de massa desconhecida em repouso. . Imediatamente após a colisão ambos adquirem a mesma velocidade . . Após a colisão, como ilustrado na figura , a componente vertical da posição do centro de massa do conjunto tem uma variação máxima igual a . Despreze atritos.
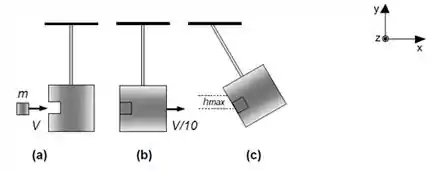
- Usando o sistema de coordenadas indicado, determine o impulso provocado pelo pêndulo no bloco, durante a colisão.
- Utilizando princípios de conservação de energia determine , a altura máxima alcançada.
- Determine a massa do pêndulo.
Passo 1
Letra a)
O impulso provocado no bloco é igual a variação do seu momento linear.
No caso do bloquinho, temos:
Onde usamos o dado do enunciado de que o bloquinho e o pêndulo adquirem uma velocidade após a colisão. Assim:
Passo 2
Letra b)
Logo após a colisão, nós podemos afirmar que a energia se conserva (já que não há forças não conservativas).
Como a energia potencial é apenas gravitacional, se tomarmos a altura inicial do pêndulo como referência, temos:
Considerando o movimento do sistema como um todo (bloquinho + pêndulo), temos:
Porém, estamos sempre considerando o centro de massa (pois o bloquinho e o pêndulo se movem junto com seus centros de massa, sem nenhum movimento relativo).
Passo 3
Letra c)
Para acharmos a massa do pêndulo, podemos usar a conservação do momento linear antes e depois da colisão, já que não há forças externas atuando ao longo dessa direção.
A conservação do momento linear fica:
Daí tiramos que:
Resposta
Letra a)
Letra b)
Letra c)