Um carrinho de massa se move sobre uma superfície sem atrito com uma velocidade = 2m/s para a direita, quando uma explosão ocorre e o carrinho se divide em duas partes: A e B. Uma parte do carrinho com massa continua a se mover para a direita com
uma velocidade . Qual a velocidade da outra parte do carrinho de massa ?
a) 4m/s para a esquerda
b) 2m/s para a esquerda
c) 1m/s para a esquerda
d) 0
e) 1m/s para a direita
Passo 1
O-LHA-A-EX-PLO-SÃO !!
Temos aqui, um caso de explosão. E explosão nada mais é do que um colisão, só que às avessas. Não é verdade ?
É sim. Então, o importante aqui é entender que vai haver conservação do momento linear, assim como nas colisões.
Vamos dar uma olhada no caso:
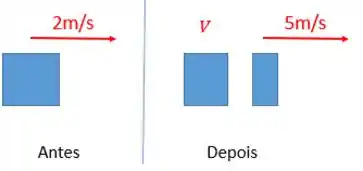
Então, bora conservar esse momento linear aí:
Como deu um valor positivo, a resposta é para a direita.
Resposta
Letra e)