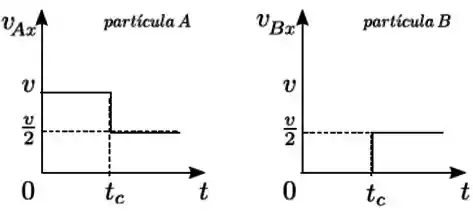
Duas partículas e de massas iguais colidem unidimensionalmente ao longo do eixo . Os gráficos a seguir representam as velocidades em função do tempo para cada partícula. Se é o momento linear do sistema formado pelas duas partículas e sua energia cinética, podemos afirmar que nessa colisão
se conserva e não se conserva
se conserva e se conserva
não se conserva e não se conserva
não se conserva e se conserva
e
Passo 1
Digamos que as partículas têm massa .
Podemos ver, pelo gráfico, que antes da colisão a partícula tem velocidade positiva e de módulo , então vamos chamá-la de .
Por outro lado, a partícula está em repouso.
Então o momento linear inicial do sistema antes da colisão é:
Passo 2
E depois da colisão, as 2 partículas têm velocidade . Então o momento linear final do sistema depois da colisão é:
Portanto, o momento linear se conserva.
Passo 3
Vamos pra energia cinética!
Inicialmente, a energia cinética do sistema é
Passo 4
E depois da colisão, a energia cinética é
Logo, a energia cinética não se conserva, que é o que acontece na maioria das colisões (ela só se conserva quando a colisão é elástica) o que caracteriza uma colisão inelástica.
Resposta
Alternativa