Duas massas de modelar deslizam sobre uma superfície horizontal de gelo, sem atrito. As massas possuem velocidades iniciais , e colidem de forma que seguem juntas com velocidade , conforme a Figura abaixo.
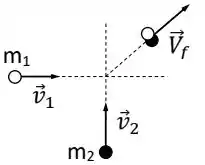
Considere as afirmativas abaixo:
I) A energia mecânica total das massas depois da colisão é a mesma que antes da colisão.
II) O momento linear total das massas depois da colisão é o mesmo que antes da colisão.
III) O momento linear da massa m1 depois da colisão é o mesmo que antes da colisão.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
a) I
b) II
c) III
d) I e II
e) I e III
f) II e III
g) Todas
h) Nenhuma
Passo 1
Como a gente já tá CANSADO de saber, a Energia Mecânica num sistema sem forças dissipativas (ou seja, sem atrito, assim como a questão nos disse) sempre se conserva. Então nossa alternativa I tá correta!
Passo 2
Assim como tem dizendo lá na teoria de colisões, qualquer tipo de colisão tem a quantidade de movimento sempre conservada! Portanto, a alternativa II também ta certa.
Passo 3
Como a gente viu no passo 2, vamos analisar essa conservação de momento linear do sistema total:
Antes temos as partículas separadas com suas respectivas velocidades, e depois, juntas com uma velocidade só, então:
Pra o momento linear da massa 1 ser conservado, essa massa precisaria ter a mesma velocidade que antes, e como acabamos de ver, não é o que acontece. Então, a alternativa III está errada.
Resposta
d) I e II