Se todas as três colisões na figura abaixo são perfeitamente inelásticas, qual ou quais geram a maior força de deformação nos carros?
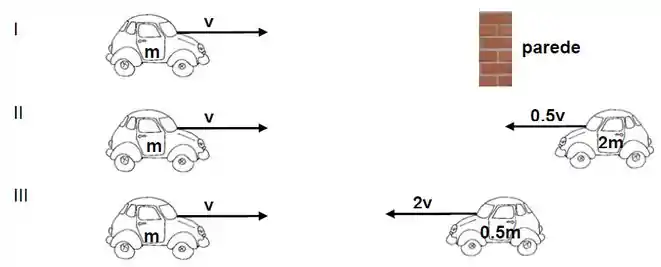
a) I.
b) II.
c) III.
d) I e II.
e) I e III.
f) II e III.
g ) todas as três.
Passo 1
Já que não se fala nada sobre atrito, podemos assumir que o único trabalho que é realizado sobre o carro é na hora da colisão, o trabalho da deformação .
E pelo teorema trabalho-energia cinética:
Ou seja:
A colisão que vai causar maior deformação nos carros é a do sistema onde, em módulo, a variação de energia cinética é maior! Tipo, se 2 carros, um andando devagar e um rápido, baterem num muro e pararem, o que estava mais rápido (com mais energia cinética) é o que vai ficar mais deformado, né? A ideia é essa!
Passo 2
Sendo a velocidade inicial do carro e sua velocidade final, a diferença de energia cinética nada mais é que:
E os de cada carro nós já temos pela imagem, então nos resta achar os , e é aí que entra o estudo das colisões.
Passo 3
Numa colisão perfeitamente inelástica, os corpos saem colados, com a mesma velocidade final . Levando isso em conta, vamos aplicar a conservação do momento linear total nas 3 colisões! Assim a gente vai achar os , beleza?
Passo 4
Colisão I:

A parede a gente tem que entender como algo gigantesco, de massa muito maior que a do carro, e que não vai se mexer depois da colisão! Então na verdade, o carro vai bater e parar.
Mas vamos dar uma olhada nas equações do movimento mesmo assim!
A parede está parada então o momento linear total logo antes da colisão é igual ao momento linear do carro:
Passo 5
Vamos chamar a massa da parede de , lembrando que consideramos .
E logo depois da colisão, os corpos se colam e saem com uma velocidade final , então:
Passo 6
Pela conservação do momento linear total:
Mas
Então dá pra considerar . Ou seja, é que nem a gente pensou no começo, o carro vai bater e parar!
Passo 7
Colisão II:

O momento linear total inicial é:
Faz sentido dar zero, porque o carro da direito tem o dobro da massa do carro da esquerda, mas metade da velocidade!
Passo 8
Como a colisão é perfeitamente inelástica, os carros saem com a mesma velocidade final e o momento linear total final é:
Passo 9
De novo usando a conservação do momento linear:
Como , isso dá:
Então os carros batem e param!
Passo 10
Colisão III:

Temos quase a mesma coisa que a colisão anterior: agora o carro da direita tem metade da massa e o dobro da velocidade, em relação ao carro da esquerda. Podemos suspeitar que o resultado vai ser o mesmo!
O momento linear total inicial é
Passo 11
E o momento linear total final é
Passo 12
Novamente vamos ter
Ou seja, nos 3 casos os carros batem e param no local da colisão!
Passo 13
Lembrando que no começo vimos:
E como nas 3 colisões , pra todos os carros envolvidos temos
Então vamos calcular a diferença de energia cinética pra todos os carros!
Passo 14
Colisão I:
O carro tem massa e velocidade , então sua variação de energia cinética é
A parede fica imóvel ao longo de todo o movimento, então sua variação de energia cinética é nula.
Portanto, a variação de energia cinética total do sistema é:
Passo 15
Colisão II:
O carro da esquerda tem massa e velocidade , então sua variação de energia cinética é
O carro da direita tem massa e velocidade , então variação de energia cinética fica:
Então a variação de energia cinética total do sistema é:
Passo 16
Colisão III:
Assim como pras outras colisões, o carro da esquerda tem massa e velocidade , logo:
Já o carro da direita tem massa e velocidade , então:
Portanto, a variação de energia cinética total do sistema é:
Passo 17
Agora só resta comparar o módulo das variações de energia cinética dos 3 sistemas! O que tiver maior módulo é o sistema onde a energia cinética variou mais, e, portanto, provocou maior deformação nos carros envolvidos:
Podemos ver que
Logo, depois desse trabalho todo podemos concluir que a colisão do sistema é a que gera maior força de deformação nos carros :)
Resposta
Alternativa (c)