Três partículas de massa estão presas a hastes de tamanho e massas desprezíveis, como uma hélice. O sistema pode girar em torno de um eixo fixo que passa pelo seu centro, , e inicialmente possui velocidade angular . Um chiclete de massa incide com velocidade conforme a figura, e realiza uma colisão perfeitamente inelástica com uma das massas .
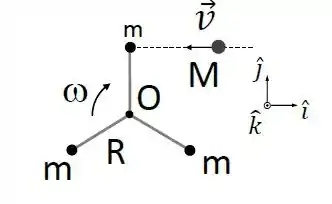
Considere que . Para que o sistema pare completamente após a colisão é necessário que tenha módulo
(A)
(B)
(C)
(D)
(E)
(F)
(G)
(H)
Passo 1
Agora a gente vai usar o fato da colisão ser inelástica!!
Colisão inelástica significa que o momento linear se conserva, e que no final da colisão os corpos saem juntos, ou seja, o chiclete grudou na bolinha e não solta mais, sacou? Ou seja, a velocidade final do chiclete e da bolinha são iguais!! ATENÇÃO!! A energia cinética não se conserva quando a colisão é inelástica.
Ele quer o módulo! Então letra C!
Passo 2
Resposta
2) C