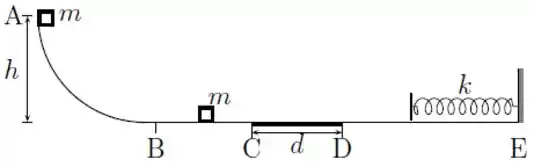
A figura mostra uma rampa com um trecho horizontal e o ponto a uma altura do trecho horizontal. Um bloco de massa é abandonado em repouso sobre a rampa no ponto e um bloco idêntico está em repouso sobre a rampa entre e .

A parte do trecho horizontal tem comprimento , e coeficiente de atrito cinético com os blocos, já o restante da rampa é totalmente liso.Ao final do trecho horizontal , entre os pontos e , encontra-se uma mola de constante elástica fixada à rampa em .O bloco abandonado em sofre uma colisão perfeitamente inelástica com o outro bloco e o conjunto se move na horizontal até atingir a mola e comprimi-la até parar.

Considere como dados e o módulo da aceleração da gravidade.

Considerando as dimensões dos blocos desprezíveis, calcule

a) a velocidade do bloco abandonado em imediatamente antes de colidir com o outro bloco;

b) a velocidade do conjunto imediatamente depois da colisão;

c) a velocidade do conjunto imediatamente antes de colidir com a mola;

d) o máximo comprimento de compressão da mola.

Como o bloco parte do repouso, sua energia cinética inicial é nula:

A energia potencial gravitacional inicial do bloco é

E o bloco não comprime nem estica nenhuma mola, então sua energia potencial elástica é nula:

Portanto,

Vamos chamar a velocidade do bloco no ponto de . Assim, a energia cinética do bloco em é:

No ponto , o bloco está no nível do chão, então sua energia potencial gravitacional é nula:

E ele continua sem contato com nenhuma mola, logo

Então obtemos

Voltando pra equação de conservação da energia mecânica:

que é aquele clássico resultado que a gente vê frequentemente nos exercícios!

Essa é a velocidade do bloco no ponto , mas como dali até ele colidir com o outro bloco não há atrito (ou outra força não-conservativa) atuando, ele vai manter essa velocidade até a colisão. Portanto, a velocidade que foi pedida é essa mesmo:

b)

Agora vamos tratar da colisão, considerando o sistema composto pelos 2 blocos.

A colisão é perfeitamente inelástica. Isso significa que os blocos vão sair da colisão colados, formando um só bloco de massa e mesma velocidade final. Da mesma forma que a gente viu agora a pouco, do ponto de colisão até o ponto não tem atrito, então vamos chamar logo essa velocidade pós-colisão do conjunto de , beleza?

E também sabemos que não tem forças externas atuando então o momento linear se conserva.

O bloco da esquerda chega com uma velocidade , enquanto o outro está parado. Então a equação de conservação do momento linear é:

c)

Do momento logo depois da colisão entre os blocos até a colisão deles com a mola, a variação da energia mecânica é dada por:

E até o conjunto chegar na mola, a única força não-conservativa que atua nele é a força de atrito, no trecho . Portanto, sendo o trabalho realizado pela força de atrito, temos

No trecho em momento algum o sistema adquire energia potencial, então sua energia mecânica é igual a sua energia cinética. E da mesma forma, sua diferença de energia mecânica é igual à sua diferença de energia cinética, logo:

Obs: usando o teorema trabalho-energia cinética chegaríamos no mesmo resultado.

A força de atrito tem módulo igual a:

Como o conjunto está na horizontal e não tem nenhum movimento vertical, a força normal e a força peso se cancelam, então

Logo,

O comprimento do trecho , que é onde atua a força de atrito, é . E a força de atrito é contrária ao sentido do deslocamento, então seu trabalho é negativo e dado por:

Logo,

Lembrando que vimos que isso dá:

Vamos manter o padrão e chamar a velocidade do conjunto no ponto de . Assim, a diferença de energia cinética no trecho é:

Substituindo e , isso dá:

Essa é a velocidade do conjunto no ponto , mas como de lá até a mola não tem atrito, essa velocidade vai permanecer constante até o momento imediatamente antes da colisão com a mola.

Então a velocidade procurada é

d)

No trajeto do conjunto enquanto ele comprime a mola até parar, podemos aplicar de novo a conservação da energia mecânica.

O conjunto chega na mola sem energia potencial, então sua energia mecânica é igual à sua energia cinética e vale:

Quando o conjunto para, ele não tem mais energia cinética. Então sua energia mecânica final é igual à sua energia potencial elástica:

sendo a compressão máxima da mola que queremos achar.

Portanto, pela conservação da energia mecânica:

Essa é a compressão máxima da mola!