Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Colisões Inelásticas

Ver Teoria
Exercício 77123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767879808182838485868788899091

Enunciado

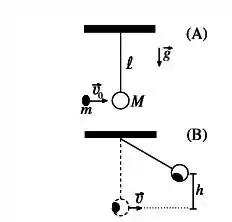
Um corpo de massa M encontra-se pendurado na vertical por uma haste de comprimento l e massa desprezível. Uma partícula de massa m   =   M / 4 atinge o corpo com velocidade v → 0 = v 0 i ^ (figura( A )). Imediatamente após a colisão os dois corpos se deslocam unidos com velocidade v → = 2,0 i ^ m / s . Considere a aceleração gravitacional no local g → = - 10 j ^   m / s 2 .

(a) Determine v 0 .

(b) Após a colisão o sistema se desloca verticalmente de uma altura h , quando fica momentaneamente em repouso (figura( B )). Calcule h .

Passo 1

a) Podemos conservar o momento linear na direção x , já que a componente da força externa resultante é nula no momento da colisão. Portanto:

p x , a n t e s = p x , d e p o i s

m v 0 = m + M v

v 0 = 1 + M m   v = 5 v

Como v = 2   m / s :

v 0 = 10   m / s

Passo 2

b) A energia mecânica é conservada entre os instantes logo depois da colisão até o sistema atingir a altura máxima, já que só forças conservativas agem. Portanto:

E a n t e s = E d e p o i s

0 + 1 2 m + M v 2 = m + M g h

Portanto:

h = v 2 2 g = 4 20 = 0,2   m

Resposta

a) v 0 = 10   m / s

b) h = 0,2   m

Exercícios de Livros Relacionados

Na Fig. 9-63, o bloco 1 (com uma massa de 2,0k g ) está se movendo para a direita com uma velocidade escalar de 10m / s e o bloco 2 (com uma massa de 5,0k g ) está se movendo para a direita com uma ve
Uma colisão frontal perfeitamente inelástica ocorre entre duas bolas de massa de modelar que se movem ao longo de um eixo vertical. Imediatamente antes da colisão, uma das bolas, de massa 3,00k g , es
Um vagão fechado em um pátio de manobras é colocado em movimento no topo de um morro artificial. O vagão desce silenciosamente e sem atrito sobre um trilho horizontal reto, onde se acopla com um vagão
Uma bala de 10,0g é disparada e entra em um bloco de madeira de 200g em repouso sobre uma superfície horizontal. Após o impacto, o bloco desliza 8,00m antes de parar. Se o coeficiente de atrito entre
Duas lontras brincalhonas deslizam ao encontro uma da outra sobre uma superfície horizontal lamacenta (e, portanto, sem atrito). Uma delas, com massa de 7,50k g , desliza da direita para a esquerda a