Resolva o que se pede:
Faça o mapa de contorno da função abaixo, mostrando várias curvas de nível:
Passo 1
Para achar as curvas de nível de uma função qualquer, sempre temos que fazer:
Assim
Daí, passando a exponencial dos dois lados, pra tirar esse , temos que
Das propriedades do logaritmo:
Ou seja, só precisamos esboçar vários gráficos dessa forma, fazendo variar o .
Passo 2
Ok, mas o que danado são esses gráficos??
Vamos dividir os dois por pra ver se isso te lembra alguma coisa:
OPA, pera aê, pera aê, pera aê...
Isso tá me lembrando a equação geral de uma elipse, que é
E, de fato, se arrumarmos só um pouquinho mais essa expressão, teremos
Ou seja, quando variamos o valor da constante , temos, portanto, elipses centradas na origem, com semi eixos em e em .
Passo 3
É só a gente arbitrar valores de e desenhar essas elipses então
Vamos arbitrar :
Que é
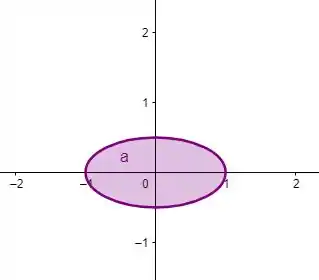
Se fizermos :
Que é
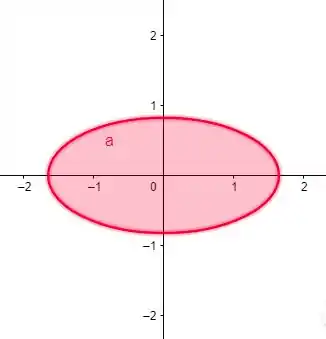
E, se fizermos :
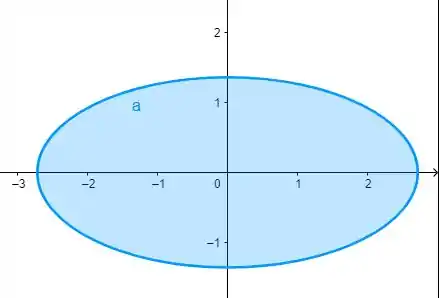
Bom, deu pra perceber então que, conforme a gente aumenta o valor de , aumentamos os semieixos da nossa elipse.
Passo 4
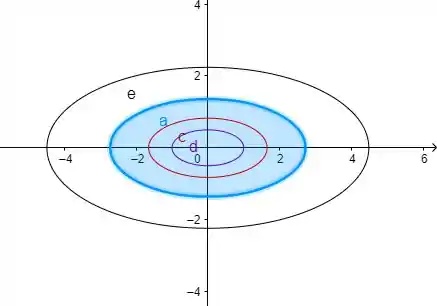
Agora, pra fazer o mapa de contorno, é só a gente desenhar todas essas elipses num desenho só, assim:
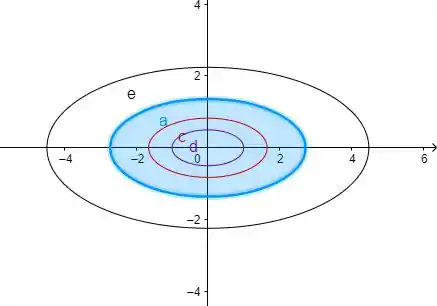
Os: repare que eu ainda desenhei mais uma elipse... Você não precisava fazer tantas, eu só fiz mais uma pra te mostrar que o mapa de contorno surge conforme a gente vai variando o valor de .
Resposta