Seja
a) Encontre e esboce o domínio de .
b) Esboce a curva de nível de que corresponde ao nível . Em que pontos essa curva intercepta o eixo ?
c) Encontre uma parametrização para a curva do item
d) Sabendo que a imagem da curva , , está contida no gráfico de , encontre a função e dê a equação da reta tangente a em .
Passo 1
a) Vamos lá, encontremos o domínio. O domínio da função é formado por todos os pontos que ela é, digamos, bem determinada, show? Isso quer dizer que não pode ter raiz com numero negativo dentro, não pode ter fração com denominador igual a , não poder ter logarítmo de , e aí por diante.
Nessa função, o que está de cara pra gente é que o denominador não pode valer , se não ela fica indeterminada! Assim,
E o domínio é o conjunto de todos os pontos de que não pertencem a essa curva!
Passo 2
Ok, agora vamos esboçar o domínio. No caso, é bem mais simples esboçar exatamente o que não faz parte dele, que é a curva do passo anterior!!
Se você observar, a curva é uma parábola!!
Como o quadrado está no , então a boca dela aponta na direção do eixo . Como o coeficiente do é positivo, , então a boca aponta no sentido positivo de :)
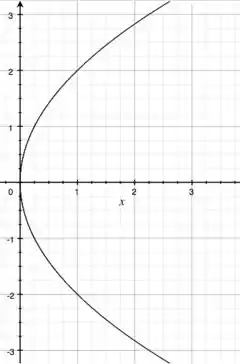
E o domínio é a parte branca, que é todo o menos a curva em preto!
Passo 3
b) Ok, agora querem a curva de nível que tem . Então, tudo o que temos que fazer é pegar a função e igualá-la a !
E agora partiu ver que curva é essa! Vamos desenvolver melhor essa equação?
Dividindo tudo por ,
Agora, o que acha de completarmos o quadrado para o ? Só pensar que o coeficiente do é duas vezes o coeficiente do vezes o segundo termo do produto notável. Assim,
E pronto! Temos aí a equação de uma elipse, centrada em !
Passo 4
Agora, analisemos o que o enunciado realmente pediu: Em que ponto essa curva corta o eixo ? Para saber disso, temos que fazer , e então teremos o ponto pedido :)
Tirando a raiz quadrada dos dois lados,
Mas tome muito cuidado agora! Encontramos os pontos e , certo? Não! Temos apenas o segundo, pois a origem não faz parte do domínio da função, lembra do ítem ? Assim, temos apenas o ponto , pois a curva não toca a origem:
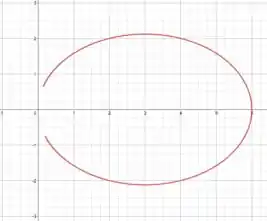
Coloquei direto a imagem da elipse, mas se você tiver alguma dúvida de como se esboça, é só lembrar da equação geral:
Então, como nosso e , seu centro está em . Aí para ver os semieixos, você pega, a partir do centro, e na direção e e na direção !
Passo 5
c) Essa veio de brinde! Partiu então parametrizar essa elipse! Claro, lembrando de excluir a origem! A dica para esse tipo de parametrização é pensar que a sua equação é exatamente igual a de uma circunferência, exceto pela parte dos denominadores do e estarem diferentes um do outro.
Aí em vez de e , teremos ! Lembrando de somar os possíveis e que venham a aparecer:
Colocando o denominador do da maneira correta, temos:
E a parametrização para a elipse será:
Ou seja, é a elipse, com sua parametrização de costume, mas com o restrito, excluindo , que daria o ponto .
Passo 6
d) Show! Como nos deram e em função do parâmetro , para descobrir , basta jogar e na equação da ! Fica assim:
E a curva fica, por fim,
Passo 7
Agora vamos encontrar a reta tangente no ponto ? Bom, antes de mais nada, vejamos que ponto é esse, colocando em :
Perfeito! Agora, derivemos a função :
E substituamos o ponto de tangência na equação da derivada, para ver qual é o vetor diretor da reta tangente:
Passo 8
Show! Prometo, mano(a), esse é o último passo :) Agora que temos o ponto de tangência, e o vetor diretor da reta tangente (que sempre será a derivada da curva no ponto de tangência), só jogar na nossa fórmula:
Ou seja, o que eu fazemos nada mais é do que esticar o vetor diretor com esse parâmetro , e levamos a reta para o ponto de tangência !
Resposta
a)
b) Corta o eixo no ponto , apenas.
c) ,
d)