Seja .
a) Esboce uma família de curvas de nível de .
b) Encontre a interseção do gráfico de com o plano e descreva a interseção do gráfico de com cada plano , em que .
c) Descreva e esboce o gráfico de .
d) Encontre uma parametrização para a interseção do gráfico de com o plano , explicitando o domínio.
Passo 1
a) Curvas de nível? Não tem nível definido? Então joguemos um nível “” e vejamos que família de curvas é essa! Igualando a , temos:
Elevando os dois lados ao quadrado, temos:
E perceba que o termo é constante! Assim, nossas curvas são todas parábolas :)
Como o quadrado está no , e seu coeficiente é positivo, ela aponta para o sentido positivo do eixo ! E vale lembrar que como o interior da raiz da equação original não pode ser menor do que , não temos curvas com nível negativo! Enfim, as parábolas ficam assim:
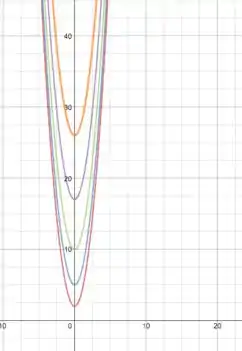
Passo 2
b) Agora vejamos a interseção do gráfico de com o plano . Para isso, apenas colocamos na equação da função! Fica assim:
Show! Chegamos numa parábola, no plano , que aponta para o sentido positivo do eixo ! Mas atenção, não tínhamos que ? Então não é a parábola toda, pois deve ser maior que (não estamos trabalhando com raízes dando números negativos)!
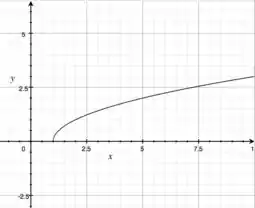
Aqui, o eixo é o vertical, e o o horizontal
Passo 3
Agora, vamos à segunda parte da letra . Vejamos quais são as curvas formadas pelos planos ! Novamente, basta colocar onde aparecer na equação de :
E aí? Percebeu que curvas são essas? Bom, de cara já vemos que deve ser maior que 1, certo? Para não haver dois números ao quadrado somados e igualados a alguma coisa menor que !
Para facilitar a vida, suponhamos ... Qual seria a curva?
Uma elipse!! Sim! E coloquei o dividido por ao invés de multiplicado por para cair certinho no nosso “template” da equação da elipse! Assim, para esse caso, seus semi-eixos são e !
E, novamente, lembrando que, como tínhamos uma raiz quadrada na parada, não podemos dizer que são elipses completas, pois se , então ! Assim, temos apenas a parte de cima das elipses!
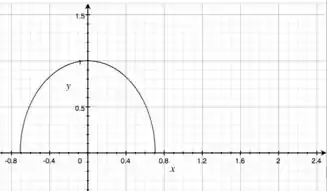
Aqui o eixo é o da vertical, e o o da horizontal!
Passo 4
c) Agora só precisamos juntar o que fizemos até agora! Temos elipses nos planos , ou seja, em planos paralelos ao , e temos parábolas nos planos , ou seja, em planos paralelos ao . Então, temos um paraboloide elíptico!
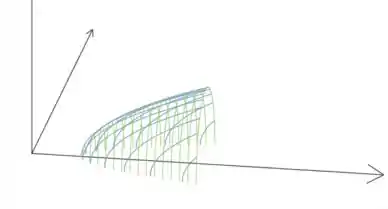
Passo 5
d) Como sabemos, a interseção entre duas superfícies, no nosso caso o paraboloide e o plano, deve nos dar uma curva! Para fazer essa interseção, como é o plano , vamos trocar todos os por na :
Show!! Acabamos de encontrar uma parábola! Agora é só parametrizar... Como temos que e são iguais, podemos chamar de e de também. Como temos em função de , que é o nosso da parametrização,
E a curva, parametrizada fica:
Beleza! E quanto aos limites do parâmetro? Ele vale para todo o ? Não! Lembra da raiz quadrada? Vimos que deve ser maior ou igual a zero, então
Resposta
a) 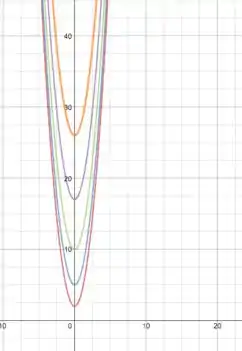
b) 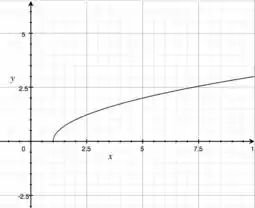
c) 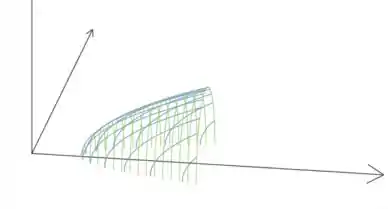
d) ,