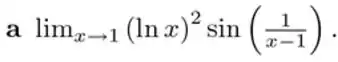
Passo 1
Começamos substituindo esse cara aí:
Indeterminação no argumento do seno! Vamos usar algum processo que elimine ela.
Passo 2
Aqui podemos usar o teorema do confronto, considerando que esse seno é uma função limitada entre e :
Multiplicando esse seno por e aplicando o limite para , teremos o seguinte:
Passo 3
Assim, calculamos os limites das pontas:
Logo,
Resposta
Exercícios de Livros Relacionados
Se 2 x ≤ g x ≤ x 4 - x 2 + 2 para todo x , encontre lim x → 1 g ( x )
Encontre lim x → ∞ f ( x ) se, para todo x1 10 e x - 21 2 e xf x5 x x - 1
Suponha que, para todo x , |g (x)| = x^4 . Calcule underset(x - 0)(lim) (g (x))/(x) .
Sejam f e g duas funções definidas em R e tais que, para todo x , g x 4 + f x 4 = 4 . Calcule e justifique. lim x → 0 x 3 g x lim x → 3 f x x 2 - 9 3
Seja f definida em R e tal que, para todo x , f x - 3 ≤ 2 x - 1 . Calcule lim x → 1 f x e justifique.