3. Use o Teorema do Confronto para mostrar que . Ilustre fazendo os gráficos, no mesmo sistema de coordenadas, , e .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nesse problema, temos que aplicar o teorema do confronto para obter o limite de para tendendo a .
Sacou? 😉
O limite de uma função é um conceito fundamental da matemática que descreve o comportamento da função à medida que a variável independente se aproxima de um determinado valor.
O Teorema do Confronto é usado para avaliar o limite de uma função quando se aproxima de um valor . A ideia do teorema é que, se conseguirmos encontrar duas funções e , ambas definidas em um intervalo que inclui , tais que:
para todos os valores de no intervalo, exceto possivelmente em . Então:
Então, podemos concluir que:
Esse teorema meu muito usado para limites de funções trigonométricas.
Legal, né? Bora começar! 😎
Passo 2
Sabemos que a função cosseno varia entre e , ou seja, é definido entre e .
Se multiplicarmos todos os lados por , vamos obter que
Assim, aplicando o limite desses lados para tendendo a , temos
Agora calculamos o limite apenas dos extremos pelo método da substituição
Substituindo na inequação...
Então, certamente
Tranquilo até aqui? 😁
Passo 3
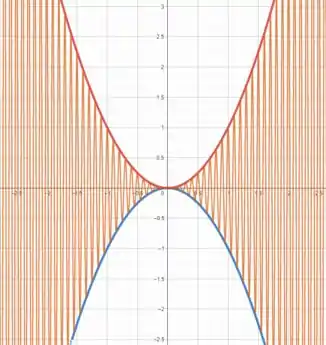
Vamos esboçar os gráficos de , e .
A função e são parábolas conhecidas onde tem concavidade voltada para baixo e tem concavidade voltada para cima.
Já a função um uma função cosseno com amplitude variável e frequência elevada .
Fim! Iae, o que achou? Responde Aí! 😁