UFCG – Cálculo Diferencial e Integral I – AV1, 2021.2 – 5
Suponha que, para todo , . Use o Teorema do Confronto para calcular
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu nos deu uma função em módulo, , que ele disse que é sempre menor ou igual a e pediu pra gente calcular o limite de usando o Teorema do Confronto? Mas o quê que diz esse teorema?
O Teorema do Confronto nos que se uma função tá espremida em um ponto entre outras duas funções, e por exemplo, tipo assim:
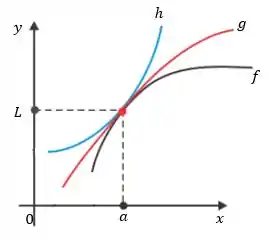
E essas duas funções tiverem o mesmo limite em , então vai ser forçado a ter o mesmo limite em . Matematicamente seria o seguinte: se quando está próximo de e , então
Beleza, e como esse Teorema me ajuda? Ele vai nos ajudar porque nós temos uma função que também é limitada, , e essa função aparece no limite dividida por . Então, nós vamos manipular essa nossa expressão pra chegar em algo parecido com , limita-la entre duas funções e assim calcular o limite .
Vamos lá!
Passo 2
Vamos começar dividindo a nossa expressão por nos dois lados:
Simplificando do lado direito:
Vamos agora colocar o módulo também em e , porque essas expressões podem assumir valores negativos:
Como já temos a nossa função , que queremos descobrir o limite, e ela está limitada, agora podemos usar o Teorema do Confronto. Podemos chamar e , então nossa função vai estar entre elas, como no passo . De modo que podemos escrever:
Vamos agora testar a condição dos limites serem iguais, ou seja, se:
Passo 3
Vamos calcular o primeiro limite, que é bem simples, basta aplicar o valor:
Agora resolvendo o segundo:
Assim, percebemos que:
Então, pelo Teorema do Confronto, podemos concluir que:
E como o limite é igual a zero, também é igual a zero.
E encerramos o exercício. Valeu, galera! 😉