Q01c) Avalie os limites abaixo e encontre o correspondente valor caso exista. Justifique suas respostas:
Passo 1
Quando a gente olha pra esse limite, ficamos um pouco confusos, porque o seno é uma função oscilatória, e:
Ou seja, esse resultado não é muito conclusivo né? Mas olha só, não importa quem seja a função dentro do seno, uma coisa é sempre verdade sobre o seno:
No nosso caso :
Se esse seno está limitado por duas funções constantes e difere de somente pelo , pelo teorema do confronto (ou do sanduíche, depende se você está ou não com fome), podemos multiplicar a inequação toda por :
E agora é só aplicar o limite:
Resolvendo os limites das extremidades:
Pô, se o limite ta entre e só pode ser então:
Passo 2
Nesse passo vou só dar uma contextualizada pra você ver o quão bonito é esse resultado. Apesar de não estar definido pra da pra ver realmente que o limite da função é :
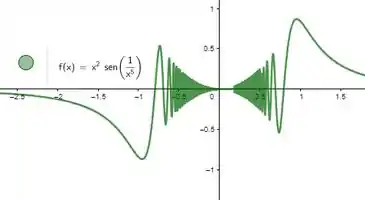
Lindo, não?