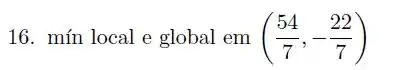![]()
Passo 1
Vamos encontrar os pontos críticos.
Assim, achando as derivadas:
Igualando a zero:
Passo 2
Isolando o na primeira equação:
E substituindo na segunda:
Assim
O ponto crítico é
Passo 3
Agora vamos classificar esse ponto crítico.
Calculando as derivadas segundas:
Como são constantes, se substituirmos elas no ponto crítico, teremos a mesmas constantes.
Passo 4
Vamos calcular o determinante:
Como e , o ponto é um ponto de mínimo local.
Passo 5
Agora entramos com o enunciado.
De acordo com o que ele disse, para funções tipo a nossa, é possível provar que se um ponto é extremante local, então também é global.
Assim, nosso ponto de mínimo local é também um ponto de mínimo global.
Resposta