[ENUNCIADO COMUM ÀS QUESTÕES 5 E 6]
Uma barra delgada de massa e comprimento é mantida na vertical com uma das extremidades apoiada no solo e depois é liberada. A extremidade superior atinge o solo sem que a extremidade de apoio deslize. Considere e que o momento de inércia de uma barra de massa e comprimento em torno de um eixo que passa pelo seu centro de massa é .
[QUESTÃO 5]
Qual é o momento angular (em ) da barra quando sua velocidade angular é ?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
A barra delgada está apoiada verticalmente no chão:
Ela vai tombar sem que seu ponto de apoio deslize.
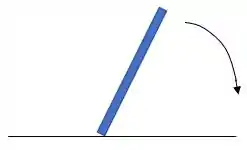
Okay!
Bom, o momento angular de um corpo extenso pode ser calculado com:
Queremos quando a velocidade angular for .
Passo 2
Então, é só substituir?
Muito cuidado, o momento de inércia da barra está com relação a um eixo passando pelo seu centro de massa:
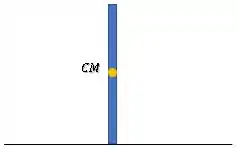
Então, precisamos aplicar o teorema dos eixos paralelos para encontrar o momento de inércia com relação ao eixo de rotação que está na base da barra.
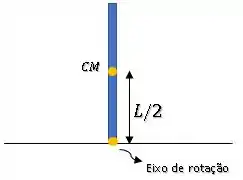
Passo 3
Agora sim, podemos encontrar o momento angular da barra com relação à sua base:
Ficamos com a letra (i).
Resposta
Letra (i)