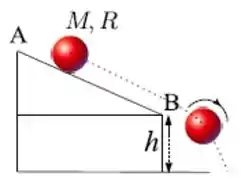
Uma esfera de massa , raio e momento de inércia , em relação ao eixo que passa pelo seu centro de massa, desce um plano inclinado (ver figura), rolando sem deslizar. A esfera parte do repouso e desce até o final do plano inclinado (ponto ), situado a uma altura em relação ao solo. Neste instante, ela tem velocidade angular , e entra em queda livre. Afirma-se que: Imediatamente antes de tocar o solo, a velocidade angular da esfera é . Imediatamente antes de tocar o solo, a velocidade angular da esfera continua com valor . O momento angular da esfera mantém-se perpendicular ao plano do movimento. Ao longo da queda livre, a energia cinética de rotação da esfera permanece constante. Qual(ais) da(s) afirmação(ões) acima está(ão) incorreta(s)?
- Somente a .
- Somente a .
- e .
- e .
- e .
Passo 1
Vamos analisar cada afirmação
Falso, A velocidade angular da esfera só muda quando temos uma força realizando torque para gerar uma aceleração angular, que só acontece quando ele está no plano inclinado. Então a velocidade angular assim que ele sai do plano vai ser a mesma de quando ela chega no fim do movimento.
Passo 2
Verdadeiro, está explicado no passo 1
Passo 3
Verdadeiro, O momento angular visto na forma de vetor tem componente sempre então ele sempre vai ser, para nós saindo ou entrando na folha.
Passo 4
Verdadeiro, Se a velocidade angular não muda consequentemente a energia cinética de rotação também não.
Resposta
Letra A