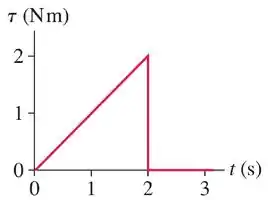
Um objeto tem momento de inércia com respeito ao seu eixo de simetria de e está sujeito a um torque paralelo ao eixo de simetria e com respeito a um ponto sobre este eixo. A magnitude do torque é mostrada no gráfico. Se o objeto está inicialmente em repouso, a magnitude da velocidade angular do objeto em é:

A.

B.

C. impossível determinar, pois o torque depende da distância do ponto de aplicação da força ao eixo de rotação e da magnitude da força.

D.

E.

Usando a equação que a gente falou ali em cima:

Como o é uma constante, pode sair da derivada:

Maravilha! Vamos olhar para o gráfico:

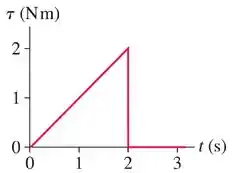
Entre e o gráfico é uma reta, ou seja:

Onde é uma constante e vale 1, já que pra cada y, o x é igual

Então:

Integrando em função do tempo nos dois lados:

constante.

Beleza, já temos uma função de .

Sabemos que pois a velocidade inicial é nula. Substituindo então:

Então já descobrimos o valor da constante D. Ficamos com:

Agora vamos calcular :

Como entre e o torque é nulo, consequentemente a aceleração angular é nula, temos que a velocidade angular é constante entre e . Então