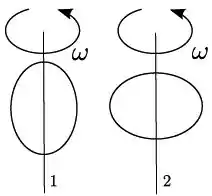
Um aro elíptico homogêneo de massa é posto para girar com velocidade ao redor do seu eixo maior, em relação ao qual tem momento de inércia . Em seguida, é colocado para girar com mesma velocidade angular ao redor de seu eixo menor, em relação ao qual tem momento de inércia . Veja as figuras. Sobre os módulos dos momentos angulares e dos aros nas respectivas situações e , podemos afirmar que:
- , pois o momento de inércia ;
- , pois trata-se do mesmo sistema girando com a mesma velocidade angular;
- , pois o momento de inércia ;
- , pois o momento de inércia ;
- , pois o momento de inércia ;
Passo 1
Lembra do exercício do bailarino? Quando mais massa estiver longe do eixo de rotação maior vai ser o momento de inércia. Dessa forma
Passo 2
O momento angular vai ser
Como as velocidades angulares são iguais
Resposta
Letra A