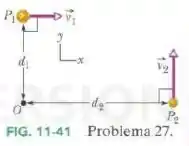
No instante da Fig. 11-41, duas partículas se movem em um plano . A partícula possui uma massa de e uma velocidade e está a uma distância do ponto . A partícula possui uma massa de e uma velocidade e está a uma distância do ponto . Quais são (a) o módulo e (b) a orientação do momento angular resultante das duas partículas em relação ao ponto ?
Passo 1
Essa é uma boa questão pra botar em prática o que você aprendeu sobre regra da mão direita!
Vamos usar o sistema de eixos dado na figura, onde o eixo aponta para fora da tela do seu computador.
Queremos o momento angular resultante, que é dado por:
Onde e são vetores que tem origem no ponto O e terminam nos pontos onde estão as partículas e , respectivamente.
Substituindo os valores das massas, bem como o módulo, direção e sentido das velocidades e das direções, temos:
Usando da regra da mão direita para calcular e :
Resposta
- Perpendicular ao plano , apontando para fora da tela.