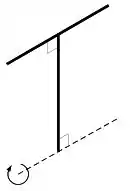
Parte I: Duas hastes iguais muito finas de comprimento e massa estão coladas em forma de um conforme ilustra a figura. O momento de inércia rotacional do conjunto em torno do eixo tracejado é:
(a)
(b)
(c)
(d)
(e) nenhuma das respostas acima.
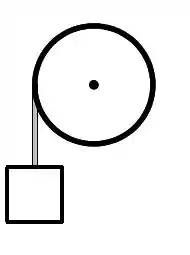
Parte II: Uma corpo de massa está conectado a uma corda que está firmemente enrolada em um cilindro de massa e raio . No instante abaixo o cilindro gira com velocidade angular e o corpo desce com velocidade de módulo igual a . A corda não desliza sobre o cilindro. Despreze a massa da corda e atritos. O módulo do momento angular do conjunto em relação ao centro do cilindro é:
(a)
(b)
(c)
(d)
(e) nenhuma das respostas acima.
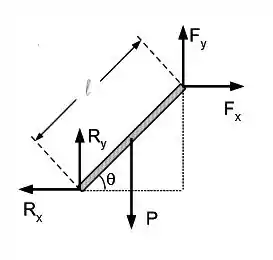
Parte III: Seja uma barra de comprimento e peso sobre a qual agem as forças ilustradas ao lado. O módulo do torque resultante em torno da extremidade superior é:
(a)
(b)
(c)
(d)
(e) nenhuma das respostas acima.
Passo 1
Parte I.
Aqui vamos usar o teorema dos eixos paralelos, então, vamos começar calculando o momento de inércia do conjunto em relação ao eixo que passa pela barra na horizontal.
Este momento de inércia é formado pelo momento de inércia da própria barra somado com o momento de inércia da barra perpendicular a ela, portanto:
Como o eixo que nós queremos calcular está distante do eixo que calculamos acima, pelo teorema dos eixos paralelos, temos:
Logo:
Resposta: letra (c)
Passo 2
Parte II.
Existem dois movimentos que irão contribuir para o momento angular: a translação do bloco para baixo e a rotação do cilindro.
Começando pela translação do bloco, temos que o vetor velocidade dista do centro do cilindro, logo:
Já para a rotação do cilindro:
Como o momento de inércia do cilindro é dado por:
E podemos tirar o ômega da relação:
Logo:
Somando os dois:
Passo 3
Parte III.
Sabemos que as forças que agem no ponto onde estamos calculando o torque não geram torque, certo? Então, vamos por partes:
Para a força peso:
Para a força :
Para a força :
Logo, somando tudo:
Resposta: letra (b)
Resposta
Parte I: (c)
Parte II: (c)
Parte III: (b)