Um spinner possui momento de inércia em relação ao eixo de simetria que passa pelo seu centro de massa. Inicialmente ele é posto para girar com velocidade angular de módulo em torno de um eixo vertical que passa pelo seu centro de massa. Em um determinado instante a pessoa que o segura muda a posição de sua mão de forma a ter um plano de rotação vertical. Com este movimento a velocidade angular do spinner é reduzida para de seu valor inicial. Qual é o módulo da variação do momento angular do spinner devido a sua mudança do plano de rotação?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Passo 1
Meio confuso imaginar cada uma dessas situações, né?
Mas inicialmente, temos que o spinner gira em torno de um eixo vertical.
Então seu momento angular também estará na direção vertical:
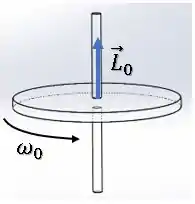
*finge que isso é um spinner* hahaha.
Porém, após o movimento da mão da pessoa, o spinner gira em um plano vertical, ou seja, seu eixo agora está na horizontal:
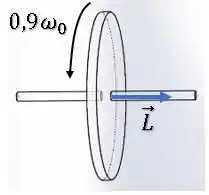
Queremos calcular o módulo do vetor variação de momento angular .
Passo 2
Sabemos que os vetores são perpendiculares:
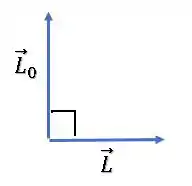
O vetor variação de momento angular é:
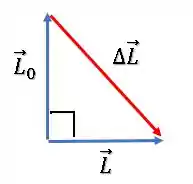
Para calcular o módulo desse vetor, basta usarmos Pitágoras:
Passo 3
O módulo do momento angular inicial será:
Como a velocidade angular do spinner é reduzida em com a mudança de orientação, seu novo momento angular será:
Substituindo esses dois valores na expressão de , temos:
Assim, temos que:
Resposta
Letra (a)