10) Calcule o fluxo do campo , através da superfície do sólido definido por , com campo de vetores normais a apontando para fora de .

O teorema basicamente é a igualdade maravilhosa:

Mas não podemos aplicar essa integral assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:

1º - Uma superfície fechada delimitando o sólido :

2º - Sem singularidades na função Vetorial:

3º - Superfície orientada positivamente:

Vem comigo averiguar essas condições ;D

1º - Uma superfície fechada delimitando o sólido :

Vamos então desenhar a superfície que queremos o fluxo. Pra começar, veja que:

Pô, essas duas inequações:

São inequações que representam regiões esféricas! A primeira seria o exterior de uma esfera centrada na origem de raio e a segunda seria o interior de uma esfera centrada em de raio . O gráfico dessas duas esferas é:

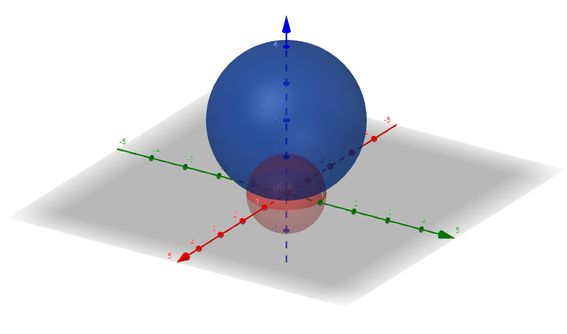
A interseção das duas inequações dá o interior da esfera azul menos a esfera vermelha. Agora, considerando , que é o interior de um cone...

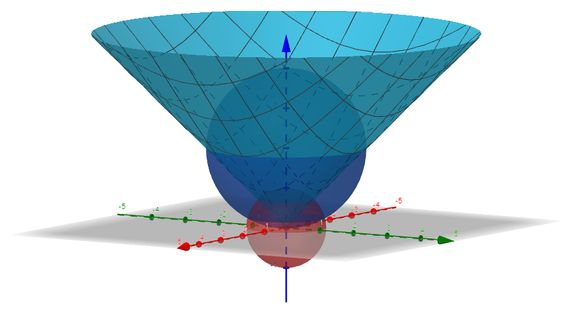
Dada a simetria dos planos e , é como se tivéssemos a seguinte região revolucionada em torno do eixo

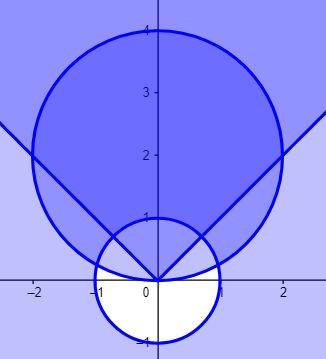
E bem, nesse caso se o sólido pode ser entendido como um sólido de revolução, a superfície é fechada! Uhuul

2º - Sem singularidades na função Vetorial:

Esse campo Vetorial funciona em todas as situações, afinal ele não tem nenhuma divisão por ou algo do tipo.

3º - Superfície orientada positivamente:

Bem, isso significa que precisamos de uma superfície com vetores normais saindo do sólido fechado por ela, o que já acontece lá do enunciado.

Bem, com as três condições sendo satisfeitas, podemos aplicar a igualdade do Teorema sem nenhuma restrição...

Então se queremos a integral de superfície, calculemos a integral tripla que cara, vai dar muito menos trabalho. Acredite em mim!

Lembra que a gente disse que nosso sólido podia ser entendido como um sólido de revolução? Oras, isso diz muita coisa pra gente! Como por exemplo, o fato de que podemos usar as mudanças para coordenadas esféricas pra resolver essa Integral Tripla:

Onde o Jacobiano dessa mudança é:

Bem, não devemos sair de uma mudança de coordenadas sem antes dizer onde os parâmetros variam. Primeiro, devemos olhar pra projeção do sólido no plano ...

Veja que essa projeção se parece muito com gráfico com um círculo. Isso ai já nos mostra o intervalo em que o ângulo varia:

Agora pro intervalo de , já que esse ângulo é definido por:

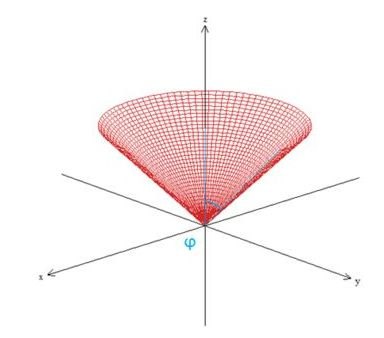
Vemos que o ângulo varia desde o eixo onde até as parede do cone definido por . Pra achar o ângulo responsável por isso, substituímos na equação do cone:

Continuando, temos que:

E o ângulo cuja tangente é será . Portanto, temos o intervalo:

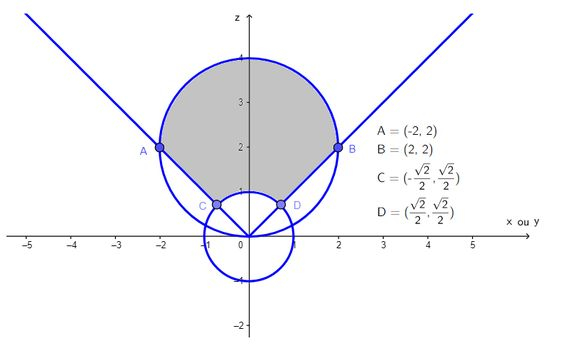
Pra fechar, vamos checar o intervalo de . Pra isso, vamos lembrar dessa linda imagem aqui que já vimos:

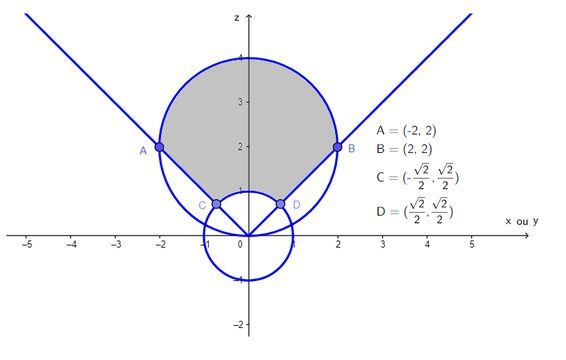
Po galera, a região cinza começa sempre na circunferência menor, ou seja, está sempre no mínimo uma unidade distante da origem. E a região cinza termina também sempre na superfície da circunferência maior! Portanto, da equação da esfera deslocada, que é a maior:

Podemos fazer as substituições:

E obter:

Sendo assim, o parâmetro vai variar da seguinte forma:

Voltando então para a integral que devemos resolver:

Realizando as substituições devidas da mudança de variáveis, e aplicando o jacobiano, temos:

Calculando a integral de dentro...

Agora a do meio...

Bora pra fechar então resolver cada uma dessas duas integrais. Pra primeira, que é mais difícil, podemos fazer a substituição:

E teremos:

O que por fim, dá:

Pra outra integral, teremos:

Juntando tudo: