Considere o campo vetorial
Seja uma constante. Determine o fluxo de através da superfície definida como a fronteira da região
Passo 1
Como o problema pede para calcularmos o fluxo de através da superfície , na verdade, ele está pedindo para calcularmos:
E como se trata de uma superfície fechada, podemos usar o Teorema de Gauss, que diz que:
Passo 2
Vamos começar calculando as derivadas parciais dos componentes de para o divergente.
Portanto,
Passo 3
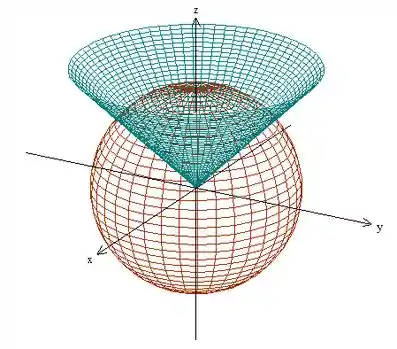
A nossa região é dada por:
Isso significa que é a região no interior da esfera
E fora do cone
O resultado é algo do tipo:
Passo 4
Como o nosso sólido é a parte de uma esfera, podemos usar coordenadas esféricas:
Vamos usar o que o problema nos disse sobre a região para descobrir os limites de , e .
Passo 5
Substituindo as coordenadas esféricas:
Passo 6
Ok, o que podemos fazer também é encontrar a interseção entre as superfícies:
Igualando os dois termos:
A interseção ocorre no plano .
Como, de acordo com as coordenadas esféricas , a interseção ocorre quando
Então podemos ver inclusive no gráfico que
Ah! Como não existem restrições para vamos utilizar os seus limites usuais:
Passo 7
Ah! Existem outras maneiras de se encontrar esse ângulo , então não precisa decorar do jeito que eu fiz.
Por exemplo, se você tenta usar só a equação:
Substituindo as coordenadas esféricas, você encontraria algo do tipo (já vou dar uma simplificada aqui, ok?):
Nesse caso,
Po! Mas deu diferente, e agora?!
Cara, fica tranquilo, estamos falando do mesmo ângulo, então relaxa.
Uma outra forma seria igualar
Substituindo as coordenadas esféricas, você encontraria algo do tipo (já vou dar uma simplificada aqui de novo, beleza?):
Considerando (na superfície da esfera):
Então
Dá no mesmo, estamos falando do mesmo ângulo.
Viu?! =]
Passo 8
Voltando pra integral:
Por substituição:
Voltando pra integral:
Onde:
Portanto: