Use o Teorema do divergente para determinar o fluxo de
Através da superfície delimitada pelo cilindro e pelos planos e com vetor normal exterior.
Passo 1
Calcular o fluxo do campo através de uma superfície é calcular a integral de superfície vetorial, e o teorema do divergente diz que a gente pode calcular essa integral pela relação:
Então a ideia é que a gente só precisa montar e calcular a integral da direita, para então achar o valor da esquerda. Maneiro, né?
Maaas a gente precisa atender a alguns critérios para podermos aplicar esse teorema:
1. Nossa superfície precisa ser fechada. Mas repara que é fechada sim. Ela é um cilindro. A base é o plano e a tampa o plano . Você pode conferir isso fazendo um esboço dessa superfície, se quiser:
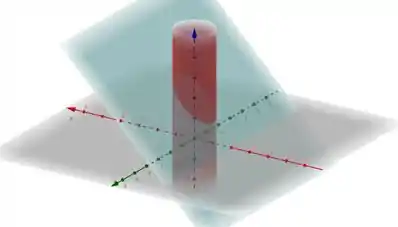
2. A superfície precisa estar orientada positivamente. E o que é isso? O vetor normal a ela deve sempre apontar para o lado de fora. E o enunciado diz isso! O vetor normal à superfície é exterior a ela.
3. O campo precisa estar bem definido para o domínio de integração. Olha ele:
Não tem nenhum ponto de descontinuidade aí né (nenhum denominador que possa zerar ou algo assim). Então a gente pode confiar que ele está bem definido para o nosso domínio de integração, já que ele está bem definido para todos os valores de .
Então, tá belezinha, a gente pode usar o teorema sem preocupações. Bora lá!
Passo 2
Vamos montar nossa integral tripla lindona:
Começando por . Esse cara é o divergente do nosso campo. Ele tem essa fórmulinha:
Como o nosso campo é:
Então a gente calcula:
Nossa integral fica:
Passo 3
A gente tem que descrever o domínio , que é essa região com formato de cilindro né? Como ela tem esse formato, nada mais justo que a gente fazer isso usando a mudança de coordenadas cilíndricas.
Isso significa que a gente vai aplicar as transformações:
Então para escrever os extremos de integração, limitamos essas variáveis que a gente tem: e .
Vamos começar observando a variável . Nesse eixo, vemos que nossa região está entre o plano e o plano . Então podemos escrever:
E aqui a gente já precisa aplicar nossa mudança de variáveis nesse :
Passo 4
E e ? Definir elas é parecido com definir uma região em por coordenadas polares. A gente viu que estamos dentro do cilindro , então podemos escrever isso em uma inequação:
Substituindo nossas transformações nessa inequação:
E como não há mais restrições, podemos assumir que os dois começam de zero e que dá a volta completa:
Belezinha?
Obs: a gente também podia limitar essas variáveis desse passo olhando o esboço da região em . Aí fica mais a seu critério mesmo. A gente chega no mesmo resultado.
Passo 5
Agora é montar a integral. Primeiro a gente substitui nossa transformação no nosso integrando:
Depois a gente multiplica o integrando por
Aí a gente pode colocar nossos extremos de integração:
Passo 6
Bora calcular essa belezura:
Aí a gente lembra daquela nossa amiga identidade trigonométrica:
Lembra que resultado era esse que a gente queria? A integral de superfície né? E finalmente a gente pode dizer que: