Dados o campo e a superfície fechada que delimita o cilindro
com a normal apontando para fora. Calcule:
(b) O fluxo de através de .
Passo 1
Nossa região está com os eixos trocados, não é aquele cilindro normal que a gente geralmente desenha no eixo , olha só como é o esboço desse aqui
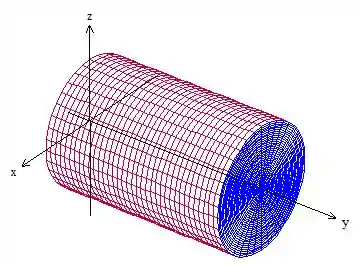
Para calcular o fluxo de precisamos da integral de superfície sobre o cilindro. Veja que temos três superfícies distintas (duas tampas e o corpo), então calcular tudo isso da forma direta vai dar um trabalho desnecessário, além do campo ser bem complexo.
Vamos pensar num outro jeito de calcular essa integral de superfície... O teorema de Gauss parece uma boa solução, já que a superfície é fechada. Vamos calcular o divergente do campo pra ver se ele é simples também
Bem mais simples, não é?
Só pra relembrar, o teorema de Gauss diz isso aqui
Onde
Passo 2
Ficou bem mais tranquilo agora né? O nosso sólido é o cilindro de raio da base igual a e altura . Isso a gente sabe pelos seus limites
Da pra calcular o volume pela integral tripla normal, mas se você se lembrar lá do ensino médio, o volume de um cilindro é simples