Calcule , onde e é a parte do cilindro acima do plano e abaixo do plano . Considere orientada com a normal que aponta para fora do cilindro.
Passo 1
Oiie, tudo bem com você?
Temos que calcular a seguinte integral de superfície
em que o campo vetorial considerado é dado por
Existe uma identificação bastante direta, através do teorema da divergência de Gauss que pode ser útil, temos que
mas note que no lado esquerdo temos uma superfície que é fronteira do sólido , em nosso caso, esse sólido é o cilindro , entre e . Para sabermos qual identificação vale a pena trabalhar, precisamos verificar a nossa superfície! Saca só!
Passo 2
A nossas região pode ser visualizada como
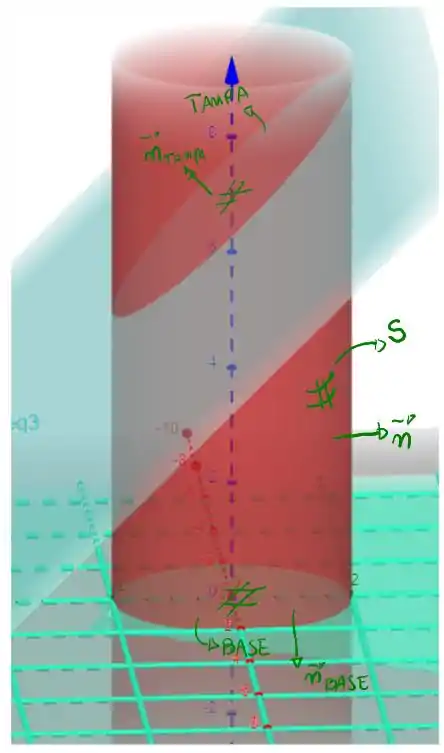
A nossa superfície é a lateral de um sólido , que tem como base o plano e tampa o plano . Então, podemos considerar o teorema da divergência de Gauss, usando um da forma
que é fronteira de , e portanto, a nossa integral pode ser identificada como
A integral que nós queremos é apenas uma parte do lado esquerdo do teorema de Gauss, portanto, vamos ter que calcular as outras três componentes. No entanto, isso é um pouco mais fácil do que expandir a integral de superfície normalmente! Saca só!
Passo 3
Vamos começar calculando o lado direito, temos que a divergência do campo é tal que
em que . Substituindo então o campo dado no enunciado, temos que
Resolvendo as derivadas parciais, obtemos que
Precisamos então resolver a seguinte integração
Portanto, só precisamos resolver as integrais de superfície! Bora lá!
Passo 4
O nosso problema está resumido em
Vamos analisar as duas integrais em conjunto, primeiro, discutindo quem são os vetores normais! Pela nossa figura, e levando em consideração que a normal considerada para a nossa superfície é tal que, temos que a tampa tem um vetor normal dado por
e, a base, analogamente, tem vetor normal
Usando o formato de nosso campo vetorial, e resolvendo os produtos escalares nas integrais de superfície, temos que
como temos que a base está em e a tampa em , por conveniência, vamos usar que , de forma que temos
Expandindo o produto no segundo termo, temos que
Ou simplesmente
Vamos tentar resolver essas integrais de superfície! Bora lá!
Passo 5
Temos que a interseção do plano com o cilindro é a seguinte circunferência
que é uma circunferência centrada em com raio . Se, usarmos coordenadas polares da forma
e
de forma que . A revolução em torno do eixo é completa, portanto, temos que , e o raio é tal que , portanto, a nossa integral é tal que
Expandindo os produtos, temos que
Vamos resolver agora as integrais todas! Vamos lá!
Passo 6
Vamos resolver primeiro as integrais em , pois algumas irão se anular, temos que
temos também que
e, por último
Portanto, temos finalmente que
Juntando alguns termos, temos que
Maravilha! Agora só falta resolver as integrais em , bora lá!
Temos que
e, também que
de forma que o resultado é tal que
Finalmente, a nossa integral é tal que
A questão foi isso! Te vejo na próxima! Tchau Tchau!