Calcule , onde e é a fronteira da região limitada pelo cilindro entre os planos e , orientada pela normal exterior.
Passo 1
Eaew, belezinha?
Precisamos calcular a integral de superfície
tendo o campo vetorial dado por
e é uma superfície que tem fronteira delimitada pela intersecção do cilindro
e, estabelecida entre os planos
e
Para resolver isso, vamos usar o teorema da divergência de Gauss, já que o campo vetorial é meio chatinho! Temos que o teorema diz
Muitas vezes é mais simples resolver a integral tripla do que calcular explicitamente a integral de superfície! Vamos lá!
Passo 2
Vamos calcular de cara a divergência do campo vetorial, temos por definição que
em que
calculando as derivadas parciais e somando todos os termos, obtemos que a divergência tem a seguinte forma
bem mais simples não é? A nossa integral se torna então
Mas, e qual é a nossa região? Vamos trabalhar com ela um pouco!
Passo 3
O sólido pode ser representado pela seguinte figura
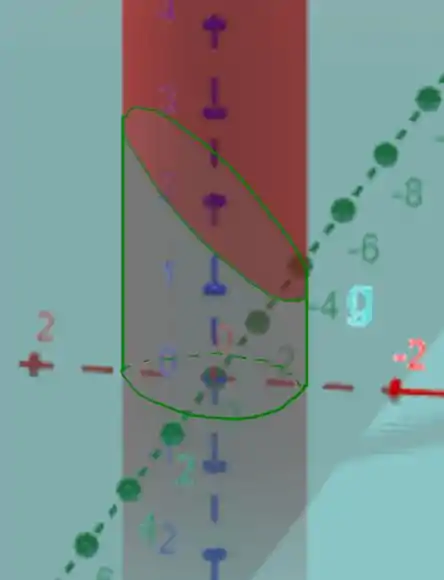
Note que este é um cilindro cortado pelo plano , portanto, podemos usar coordenadas cilíndricas para descrever a região mais fácilmente, usando que
, e
lembrando que em coordenadas cilíndricas temos . Note que , e que . Mas, a coordenada , obedece o intervalo
ou melhor
Nossa integral se torna então
Integrando primeiramente em , temos que
Avaliando os limites, temos que
Expandindo nós temos então as seguintes integrais
Podemos juntar algumas integrais para obter que
Ainda precisamos resolver nas outras duas direções! Mas para isso, será mais conveniente usarmos coordenadas polares! Vamos lá!
Passo 4
Em coordenadas polares, temos que
Vamos resolver primeiro as integrais em , temos que
avaliando os limites, obtemos que
Temos agora a segunda integral como
avaliando os limites
Temos a seguinte integração que utilizar uma substituição simples
feita da seguinte forma
e
nestas condições temos que e , como os limites são iguais, necessariamente a integral se anula! Portanto
Temos também a integral
e, por último, temos que
Juntando todos os resultados, resta a seguinte integração para ser resolvida
Vamos resolver as integrais que faltam agora!
Passo 5
Finalmente, integrando em , temos que
Fazendo um MMC, temos que o resultado final é
A questão foi isso! Te vejo na próxima! Tchau Tchau!