Seja um campo vetorial de classe em Analise as seguintes afirmações.

(I) Se então é conservativo.

(II) Se é gradiente então .

(III) Se então .

Podemos afirmar que:

a) apenas as afirmações (II) e (III) são verdadeiras.

b) todas as afirmações são verdadeiras.

c) todas as afirmações são verdadeiras.

d) apenas as afirmações (I) e (II) são verdadeiras.

e) apenas a afirmação (I) é verdadeira.

(I) Ele diz que se o rotacional zera, temos que é conservativo. Cara, vamos lá. Uma característica que o campo conservativo tem é essa:

Integral de linha vetorial sobre uma curva fechada é nula. Vamos ver se a gente consegue provar que isso é verdade para o nosso campo. E como a gente não tem a expressão do campo, mas tem o rotacional dele, vamos usar o teorema de Stokes.

Ele diz isso aqui:

Onde é a fronteira de uma superfície bem definida no domínio do campo. Se o rotacional zera, temos que:

E isso prova que o campo é de fato conservativo, né? Mas muita calma nessa hora! A gente já viu que usando o Teorema de Stokes a gente prova que o campo é conservativo.

Mas será que podemos usar o Teorema no nosso campo mesmo ele não estando definido na origem?

Vamos avaliar isso então. Lembra que no se o nosso campo tivesse rotacional nulo, mas não estivesse definido na origem, ele não era conservativo? Isso acontecia porque a gente não conseguia fazer todas as integrais sobre uma curva fechada nele zerar.

E onde estava o problema? Usávamos o teorema de Green para provar que integrais sobre curvas que enlaçavam o nosso ponto não definido ficavam diferente de zero. Aí a agora gente vai ver se isso é um empecilho aqui também. Será?

Vamos testar então se a gente consegue provar pelo Teorema de Stokes que as integrais de linha vetorial sobre curvas fechadas em volta do ponto serão nulas no .

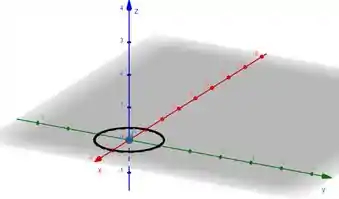
Imagina que a gente tem um círculo genérico em volta da origem. E queremos usar Stokes para calcular a integral de linha sobre ele. Precisamos de uma superfície que seja limitada pela curva, mas que não passe no ponto .

A gente pode usar uma semiesfera né?

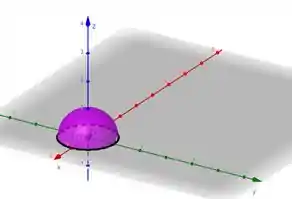
Olha só, deu certo. Aí a gente pode atender todos critérios de Stokes. Temos nossa curva que é fronteira de uma superfície que está no espaço onde nosso campo está bem definido.

Então se a gente generalizar e colocar qualquer curva fechada ali, só precisamos de uma superfície, com fronteira nessa curva que desvie de . Então de fato, Stokes vale para todo esse campo. E aí já que nosso .

E sim, é suficiente para que esse campo seja conservativo.

Verdade essa afirmação bonita.

(II) Aqui a gente tem essa informação para analisar:

Essa daí diz que se é gradiente, ou seja, , temos que

O que a gente sabe sobre ? Cara, ele só não é definido em .

Será que porque o rotacional é nulo, o divergente também vai ser? Vamos tentar pensar em um campo que tem rotacional nulo e não está definido na origem. Isso é o mesmo que criar um campo a partir de uma função potencial.

Se a nossa função potencial for, por exemplo:

Repara que ela já começa não sendo definida em . O campo que é igual ao gradiente dessa função é:

Ele tem nulo (por ter uma função potencial). Será que ele tem divergente nulo? Vamos ver:

Ih olha só. Não deu zero. Isso quer dizer que:

O que mostra que essa afirmação é falsa. ☹

(III) Essa daí diz basicamente a recíproca da outra. Se , temos . Mas será que é verdade?

Vamos usar o mesmo método e pensar em um campo que tenha , mas possa ter rotacional não nulo. Vamos tentar o campo:

O divergente dele é:

Será que o rotacional dele vai ser um vetor nulo?

Ih olha só. Não foi um vetor nulo. O que mostra que essa afirmação é falsa também. ☹

Obs: Repara que a gente escolheu um campo que não tinha só funções de na componente , só funções de na componente e só funções de na componente . Com isso, tínhamos mais chances de não zerar o .