Calcule , sendo que e é a semi-esfera com , orientada com a normal tal que .

A nossas região pode ser visualizada como

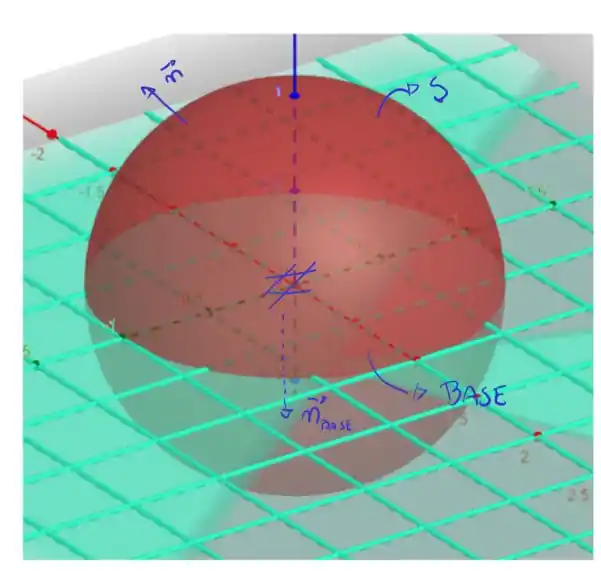
A nossa superfície é a cúpula de um sólido , que tem como base o plano . Então, podemos considerar o teorema da divergência de Gauss, usando um da forma

que é fronteira de , e portanto, a nossa integral pode ser identificada como

A integral que nós queremos é apenas uma parte do lado esquerdo do teorema de Gauss, portanto, vamos ter que calcular as outras duas componentes. No entanto, isso é um pouco mais fácil do que expandir a integral de superfície normalmente! Saca só!

Vamos começar calculando o lado direito, temos que a divergência do campo é tal que

em que . Substituindo então o campo dado no enunciado, temos que

Aplicando a regra do quociente junto com a regra da cadeia, e lembrando que em derivadas parciais toda variável que não é derivada é tomada como constante, obtemos que

evidenciando o denominador, e o termo , temos que

Portanto, temos que

sendo assim, o lado direito do teorema de Gauss é identificado como

Vamos resolver o lado esquerdo agora! Saca só!

O nosso problema está resumido em

Vamos analisar a integral de superfície que falta, primeiro, discutindo quem é o vetor normal! Pela nossa figura, e levando em consideração que a normal considerada para a nossa superfície é tal que (ou seja, o vetor normal externo a superfície ), temos que a base tem um vetor normal dado por

Usando o formato de nosso campo vetorial, e resolvendo o produto escalar na integral de superfície, temos que

como temos que a base está em isso se resume à

A questão foi isso! te vejo na próxima! Tchau Tchau!