Questão 3: Considere o campo vetorial no sólido limitado por e .
- Parametrize as duas partes das superfícies que delimitam este sólido.
- Usando as parametrizações do item anterior, calcule o fluxo de através (isto é, calcule sem usar o Teorema de Gauss).
- Calcule o divergente do campo e use o Teorema de Gauss para verificar o resultado do item anterior (isto é, calcule novamente o fluxo usando o Teorema de Gauss).
Passo 1
Item I)
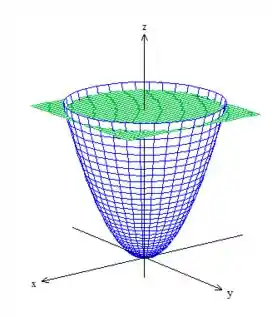
Pois bem, vamos começar desenhando a superfície desse sólido :
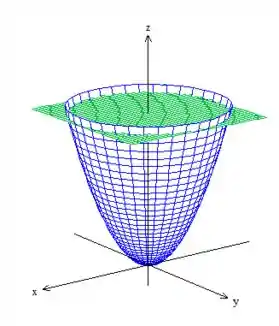
Então repare que o sólido está no interior desse bombom de cabeça para baixo !
Passo 2
Como o sólido é delimitado por duas superfícies que tem o explicitamente em função dos parâmetros, podemos fazer duas parametrizações explícitas:
No caso do paraboloide, qualquer ponto dele pode ser obtido dado um e um :
Onde :
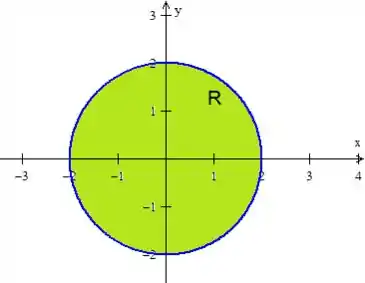
No caso, os parâmetros e estão limitados pelo plano , então:
Um círculo de raio :
Passo 3
Agora, no caso do plano , também temos uma parametrização bem semelhante, pois podemos encontrar todos os pontos do plano assim:
Onde o e o também estão delimitados pelo círculo de raio , devido a intersecção com o paraboloide:
Passo 4
Item II)
O fluxo de um campo em uma superfície é dado por uma integral de superfície:
Como a superfície é formada pelo paraboloide e pelo plano :
Vamos, então, calcular cada uma dessas integrais de superfícies e resolver o nosso problema !
Passo 5
Começando com...
Primeiro devemos parametrizar a superfície do Paraboloide, que por sorte já está feito:
Segundo, devemos calcular o termo :
Onde , dado , é dado por:
Considerando o vetor Normal para baixo (saindo):
Terceiro, substituindo o campo :
Logo, substituindo tudo na integral de superfície:
Esse , é porque agora estamos integrando no domínio de :
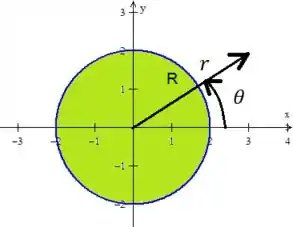
ORA! Se estivermos trabalhando com uma região circular, é útil trabalhar com as coordenadas polares:
E os limites do raio e do ângulo dependem da região :
Passo 6
Agora vamos calcular
Novamente, primeiro a parametrização:
Segundo, o termo :
Onde , dado :
Considerando o vetor Normal para cima (saindo):
Terceiro, substituindo o campo :
Logo, substituindo tudo na integral de superfície:
Como a região é um círculo de raio ...
Passo 7
Concluímos então que o fluxo através da superfície é:
Passo 8
Item III)
Seguindo o enunciado, vamos calcular o divergente primeiro:
Então:
Então, pelo Teorema de Gauss:
Como o sólido é limitado e pela superfície fechada, o campo não tem nenhuma singularidade, e ainda considerando os vetores para fora de , podemos aplicar a igualdade de Gauss sem problemas !
Ora, para calcular essa integral tripla, precisamos descrever o sólido :
Podemos adotar para isso as coordenadas cilíndricas:
Para a variação de e , já comentamos anteriormente que eles variam na projeção do sólido no plano :
Portanto:
Enquanto o ...
Onde o paraboloide é enquanto que o plano é :
Então, substituindo tudo e não se esquecendo das coordenadas polares...
Integrando então...
Resposta
Item I)
Item II)
Item III)