Considere o campo de vetores e a superfície S definida pelo hemisfério e pelos planos . Use o teorema da Divergência para calcular o fluxo
de F ao longo de S. Lembre que é o campo normal (exterior) unitário de S.
Passo 1
Para começar vamos entender a região que estamos trabalhando, tudo bem?
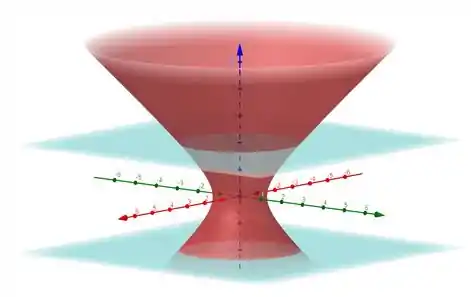
Bom, pelo teorema, precisamos ter uma superfície fechada. Como é possível ver pela figura acim,a isso pra gente não vai ser um problema.
Temos que ter ainda a orientação positiva e o campp sem singularidades. O campo que estamos trabalhando é o , o que não tem problema nenhum.
Passo 2
Com tudo isso conferido, podemos finalmente partir para nosso teorema, que nos da:
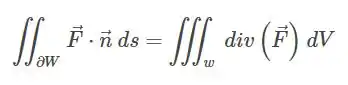
Onde nesse caso,
Podemos entçao calcular a integral tripla. Vamos começar pelo divergente.
Passo 3
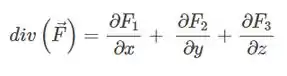
Logo,
Passo 4
Então montando a integral teremos:
Vamos então agora precisar escrever os parâmetros de variação. Pra essa questão o melhor pe fazer uma substituição para coordenadas cilíndricas:
Pela imagem percebemos que o varia entre, no entanto precisamos ainda descobrir a variação do r. Para isso, substituímos os valores de x e y dentro da superfície.
Bom, com isso vemos que r varia entre 0 e .
Passo 5
Montando e resolvendo a integral ficamos com (sem esquecer de escrever o campo em função da mudança de coordenadas):
Resolvendo primeiro a integral de fora
Voltando pra integral ficamso com:
A partir disso nós já ficamos com: