Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Gauss

Ver Teoria
Exercício 66123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646567686970717273747576777879808182

Enunciado

Considere a região do espaço euclidiano E ⊂ R 3 limitada pelas superfícies regulares dadas pelas equações:

x 2 + y 2 = 1 ;                 z + y = 1 ;                 z + y = 0

Calcule a integral de superfície

∬ ∂ E   F d S

Do campo espacial F x ,   y ,   z = x y + sin 2 ⁡ y z ,   x y + e x 2 + z 2 , z 2 2 ,   onde a superfície ∂ E está orientada positivamente.

Passo 1

Então, a primeira coisa que temos que fazer quando nos deparar com um problema desses é fazer um esboço da região E . Bora?

Bem, o sólido E é delimitado pelo cilindro x 2 + y 2 = 1 que tem o raio 1 e está centrado em z . Show?

Mas e esses planos aí? Como desenha-los?

Então, vamos começar falando do plano z + y = 1 . Repare que ele é paralelo ao eixo x (pois ele não tem x na equação ), assim basta você desenhar a equação dessa reta no plano y z e depois puxá-la na direção de x pra cima:

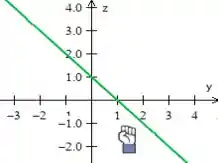
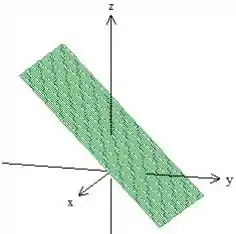
O outro plano ficará do mesmo jeito só que um pouquinho abaixo (passando pela origem). Mas enfim, desenhando todo mundo junto:

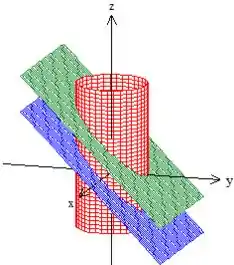
O sólido E que queremos é esse do interior aí, percebeu? As bordas ∂ E são as superfícies que estão delimitando !

Passo 2

Pow, note que o exercício esta nos dando pistas de como resolver o nosso problema: teorema de Gauss.

Por quê? Bem, porque para começar, o campo F não é fácil, as superfícies, cones e planos, vish! Menos ainda. Além disso, estamos trabalhando com superfícies fechadas, percebeu?

Mas para a gente ter certeza vamos averiguar o divergente pela fórmula:

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z

Dado que F x ,   y ,   z = F 1 ,   F 2 ,   F 3 = x y + sin 2 ⁡ y z ,   x y + e x 2 + z 2 , z 2 2 , teremos:

d i v   F → = y + x + z

Man!!! Muito mais easy! Vamos aplicar Gauss!:)

Passo 3

O teorema de Gauss relaciona:

∬ ∂ E   F d S = ∭ E   d i v   ( F → ) d V

Desde que a superfície ∂ E seja fechada (confere! ), orientada positivamente (confere! ) e o campo não tenha nenhuma singularidade (confere também! ).

Então, bora montar a integral tripla?

Passo 4

A primeira coisa é descrever a região E . Como estamos dentro de um cilindro, vamos descrever a região como coordenadas cilíndricas, se lembra?

x = r cos ⁡ θ

y = r sin ⁡ θ

z = z

O jacobiano dessa mudança é

J = r

Toda mudança de coordenadas nos obriga a descrever a variação dos novos caras:

A variação de r , como ele está dentro do cilindro, a gente pode falar que ele vai de 0 ao raio limite: ao raio do cilindro, logo:

0 ≤ r ≤ 1

Enquanto ao θ , dá uma volta completa no cilindro, logo:

0 ≤ θ ≤ 2 π

z varia entre os planos:

P l a n o   a z u l ≤ z ≤ P l a n o   v e r d e

- y ≤ z ≤ 1 - y

Substituindo y pelas novas coordenadas

- r sin ⁡ θ ≤ z ≤ 1 - r sin ⁡ θ

Passo 5

Substituindo tudo na integral tripla:

∭ E   d i v   ( F → ) d V = ∭ E   y + x + z d V =

Trocando essas variáveis pelas novas...

= ∭ E   r cos ⁡ θ + r sin ⁡ θ + z r   d z d r d θ =

Substituindo E

∫ 0 2 π ∫ 0 1 ∫ - r sin ⁡ θ 1 - r sin ⁡ θ r cos ⁡ θ + r sin ⁡ θ + z   r   d z d r d θ =

∫ 0 2 π ∫ 0 1 ∫ - r cos ⁡ θ 1 - r cos ⁡ θ ( r 2 sin ⁡ θ + cos ⁡ θ + r z ) d z d r d θ

Resolvendo a integral de dentro em z considerando as demais variáveis constantes...

∫ 0 2 π ∫ 0 1 r 2 z sin ⁡ θ + cos ⁡ θ + r z 2 2 - r sin ⁡ θ 1 - r sin ⁡ θ d r d θ =

Substituindo os limites em z

∫ 0 2 π ∫ 0 1 r 2 sin ⁡ θ + cos ⁡ θ + r 1 - r sin ⁡ θ 2 2 - r - r sin ⁡ θ 2 2 d r d θ =

∫ 0 2 π ∫ 0 1 r 2 sin ⁡ θ + cos ⁡ θ + r - 2 r 2 sin ⁡ θ 2 d r d θ =

∫ 0 2 π ∫ 0 1 r 2 sin ⁡ θ + cos ⁡ θ + r 2 - r 2 sin ⁡ θ d r d θ =

∫ 0 2 π ∫ 0 1 r 2 cos ⁡ θ + r 2   d r d θ =

Calculando agora essa integral do meio...

∫ 0 2 π r 3 3 cos ⁡ θ + r 2 4 0 1 d θ =

∫ 0 2 π 1 3 3 cos ⁡ θ + 1 2 4 d θ =

∫ 0 2 π 1 3 cos ⁡ θ + 1 4 d θ =

Integrando em θ

1 3 sin ⁡ θ + 1 4 θ 0 2 π =

Por fim, substituindo os limites em θ que a gente acabou de integrar

1 4 2 π = π 2

Resposta

∬ ∂ E   F d S = π 2

Exercícios de Livros Relacionados

Nos Exercícios 1-4, encontre a divergência do campo.4. O campo de velocidade da Figura 16.13.
Nos Exercícios 1-4, encontre a divergência do campo.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
(Divergente em coordenadas polares) Seja Ω um campo aberto no semiplano y0 e seja F → x , y = P x , y i → + Q x , y j → , x , y ∈ Ω , com PeQ de classe C 1 . Seja P 1 θ ,ρ = P x , y e Q 1 θ ,ρ = Q x ,