Sejam um campo vetorial em e uma pirâmide de vértices , onde e . Calcule o valor de sabendo que
Onde é a superfície da pirâmide , é a face de vértices , e é o campo de vetores normais apontando para fora da pirâmide.
Passo 1
Vamos fazer um desenho disso aqui rapidinho para entender melhor. Nós só conhecemos dos vértices da pirâmide: e . Unindo esses pontos, temos esses segmentos em vermelho na figura abaixo.
Sobre o terceiro vértice, , nós só sabemos que se encontra no plano , vamos desenhar um ponto qualquer desse tipo:
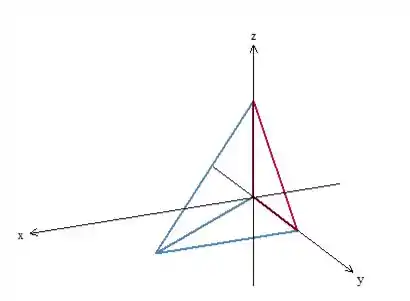
A parte que “conhecemos” da pirâmide está em vermelho e a que não conhecemos está em azul.
Passo 2
O problema nos diz então que a integral de superfície de sobre a superfície da pirâmide, somada à integral sobre a face (em vermelho) é igual a :
Vamos então calcular isso aí e tirar o valor de , ok?
Vamos começar pela integral na face . Podemos parametrizá-la como:
Isso porque a superfície pertence ao plano . Os parâmetros e , nós tiramos da projeção da superfície no plano , que, no caso, é o próprio triângulo.
Podemos dizer que varia entre e a reta inclinada que liga os pontos e , ou seja, a reta . Portanto, .
Pela própria figura, vemos que .
Passo 3
Agora nós calculamos a normal
Porém, como o problema diz que a normal aponta para fora da pirâmide, queremos o vetor oposto a esse:
Passo 4
Agora, vamos aplicar a fórmula:
Escrevendo o campo nas variáveis da parametrização:
Trazendo os valores que temos para a integral:
Passo 5
Agora, vamos calcular a outra integral de superfície. Bem, como se tratam de muitas superfícies, vale à pena usar o Teorema de Gauss aqui.
Como a região limitada por é fechada, sendo orientada positivamente, podemos aplicar o Teorema de Gauss:
Passo 6
Agora precisamos calcular . Temos:
Passo 7
Agora vamos montar a integral
Onde é o volume que vimos no passo 1.
Lembra da fórmula do volume de um pirâmide? É o seguinte:
Beleza? Calcular a área da base é tranquilo, porque temos um triângulo retângulo:
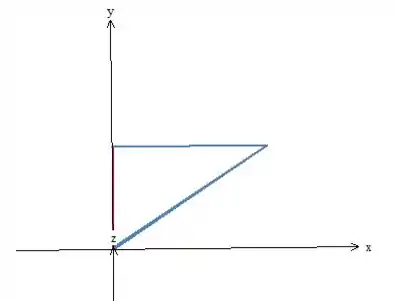
A medida de um cateto é (o vermelho) e a do outro é (o azul), pois é a coordenada do ponto . Então:
A altura da pirâmide é igual a , como podemos ver no desenho. Isso nos dá:
Portanto
Passo 8
Como
Temos