Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Gauss

Ver Teoria
Exercício 14123456789101112131516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182

Enunciado

Teorema de Gauss

Seja S a união das superfícies S 1 S 2 e S 3 dadas pelas equações abaixo:

S 1 : y = x 2 + z 2 ,     0 ≤ y ≤ 1 ;

S 2 : 1 = x 2 + z 2 ,     1 ≤ y ≤ 2 ;

S 3 : y = 3 - x 2 + z 2 ,     2 ≤ y ≤ 3 ;

Calcule ∬ S F → . n →   d S , onde F → é o campo de vetores definido por F → x , y , z = ( e cos ⁡ z ,   z 2 y + ln ⁡ x 2 + 1 ,   y 2 + x 2 z ) e n → é o campo de vetores normais unitários exterior à região limitada por S .

Passo 1

Vamos tentar imaginar como é o gráfico dessa superfície.

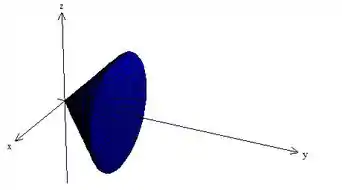
S 1 é um cone que tem o seu vértice na origem e vai aumentando o raio conforme o valor de y aumenta, até o ponto em que y = 1 , fazendo com que o raio do cone também valha 1 .

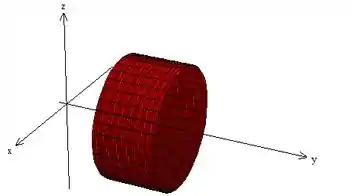
S 2 é um cilindro de raio 1 que começa no final do cone S 1 e vai até o ponto em que y = 2 .

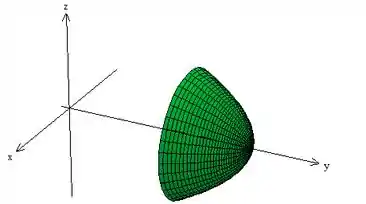
S 3 é um paraboloide que “termina” em y = 3 e começa em y = 2 , partindo do final do cilindro S 2 .

Juntando tudo, temos o seguinte:

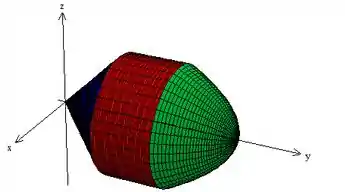
Como podemos ver, a superfície é toda fechada.

Para calcular ∬ S F → . n →   d S sobre uma superfície fechada, podemos usar o Teorema de Gauss.

Passo 2

O Teorema de Gauss é dado por:

∬ ∂ W   F → . n →   d s = ∭ w   d i v F →   d V

Onde:

d i v F → = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

Passo 3

F → x , y , z = ( e cos ⁡ z ,   z 2 y + ln ⁡ x 2 + 1 ,   y 2 + x 2 z )

F 1 = e cos ⁡ z → ∂ F 1 ∂ x = 0

F 2 = z 2 y + ln ⁡ x 2 + 1 → ∂ F 2 ∂ y = z 2

F 3 = y 2 + x 2 z → ∂ F 3 ∂ z = x 2

O divergente será:

d i v F → = x 2 + z 2

Passo 4

∬ S   F → . n →   d s = ∭ w   x 2 + z 2 d V

Podemos escrever a região W como:

W = x 2 + z 2 ≤ 1 ,     x 2 + z 2 ≤ y ≤ 3 - x 2 + z 2

Pra simplificar o nosso cálculo, podemos usar coordenadas cilíndricas, onde:

x = r cos ⁡ θ

y = y

z = r sen ⁡ θ

J = r

Os limites para x e z são tranquilos, para descobrirmos os limites para y , basta substituir na relação que eu escrevi em W . Os limites são dados por:

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

r ≤ y ≤ 3 - r 2

Passo 5

Assim, a integral tripla será:

∭ w   x 2 + z 2 d V = ∫ 0 2 π ∫ 0 1 ∫ r 3 - r 2 r 2 r   d y d r d θ

= ∫ 0 2 π ∫ 0 1 ( 3 - r 2 - r ) r 2 r   d r d θ

= ∫ 0 2 π ∫ 0 1 3 r 3 - r 5 - r 4   d r d θ

= ∫ 0 2 π 3 r 4 4 - r 6 6 - r 5 5 0 1 d θ

= 2 π 3 4 - 1 5 - 1 6 = 23 π 30

Resposta

∬ S   F → . n →   d s = 23 π 30

Exercícios de Livros Relacionados

Nos Exercícios 1-4, encontre a divergência do campo.4. O campo de velocidade da Figura 16.13.
Nos Exercícios 1-4, encontre a divergência do campo.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
(Divergente em coordenadas polares) Seja Ω um campo aberto no semiplano y0 e seja F → x , y = P x , y i → + Q x , y j → , x , y ∈ Ω , com PeQ de classe C 1 . Seja P 1 θ ,ρ = P x , y e Q 1 θ ,ρ = Q x ,