Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Gauss

Ver Teoria
Exercício 39123456789101112131415161718192021222324252627282930313233343536373840414243444546474849505152535455565758596061626364656667686970717273747576777879808182

Enunciado

5) Calcule o fluxo do campo F → = x + cos ⁡ x ,   y + y sin ⁡ x ,   2 z , através do tetraedro limitado pelos planos coordenados e plano x + y + z = 1 , onde n → é o normal unitária exterior a S .

Passo 1

Se o problema nos pediu fluxo de F → sobre uma superfície S , com toda certeza o que ele está buscando é que façamos uma integral de superfície:

∬ S   F → ⋅ d S →

Para resolver essa integral, poderíamos seguir basicamente 2 caminhos:

1º - Fazer de uma forma direta (parametrizando e tudo mais)

2º - Aplicar o Teorema de Gauss.

Veja você que o campo é um pouco complicado para se fazer uma integral de superfície direto com ele. Além disso, se você quer mais certeza ainda que de fato vamos resolver o problema pelo Teorema de Gauss, calcule o divergente...

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 2 ∂ z

Como

F → = x + cos ⁡ x ,   y + y sin ⁡ x ,   2 z = F 1 ,   F 2 ,   F 3

Calculando as derivadas parciais:

∂ F 1 ∂ x = 1 - sin ⁡ x

∂ F 2 ∂ y = 1 + sin ⁡ x

∂ F 2 ∂ z = 2

Logo...

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 2 ∂ z = 4 - sin ⁡ x + sin ⁡ x =

4

Pow, com um divergente simples desses... Sim, o problema está pedindo que façamos por Gauss!

Passo 2

O teorema basicamente é a igualdade maravilhosa:

∬ S   F → ⋅ d S → = ∭ W   d i v   F →   d V

Mas não podemos aplicar essa integral assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:

1º - Uma superfície fechada S delimitando o sólido W :

Se desenharmos S como o problema nos sugeriu, ou seja, a intersecção do plano x + y + z = 1 (representado em laranja) com os planos coordenados:

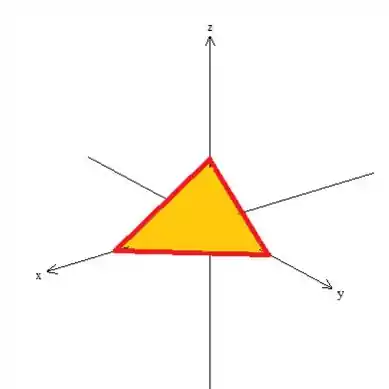
Yes! A superfície é fechada e delimita o tetraedro dentro dela !

2º - Sem singularidades na função Vetorial:

x + cos ⁡ x ,   y + y sin ⁡ x ,   2 z

Esse campo Vetorial funciona em todas as situações, afinal ele não tem nenhuma divisão por 0 ou algo do tipo.

3º - Superfície orientada positivamente:

Bem, isso significa que precisamos de uma superfície com vetores normais saindo do sólido fechado por ela, o que já acontece lá do enunciado.

Passo 3

Bem, com as três condições sendo satisfeitas, podemos aplicar a igualdade do Teorema sem nenhuma restrição...

∬ S   F → ⋅ d S → = ∭ W   d i v   F →   d V

Então se queremos a integral de superfície, calculemos a integral tripla que cara, vai dar muito menos trabalho. Acredite em mim!

Passo 4

Essa integral tripla que gerou é igual a 4 vezes o volume de W :

∭ W   4   d V = 4 ∭ W   d V = 4 ⋅ V W

Porém eu não sei você, mas eu não lembro a fórmula do volume de um tetraedro de có, ou seja, essa informação pra gente não serve de muita coisa, neh? Principalmente em uma prova que já tem muita coisa pra memorizar. Então vamos resolver na marra mesmo, ou seja, primeiro descrever a região como do tipo 1 :

Repare que o Tetraedro tem o x e y variando na projeção dele no plano x y :

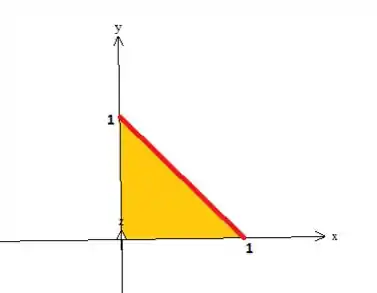
Veja que essa reta azul mais escura é o limite dele é justamente onde o tetraedro encontra o plano z = 0 , então...

x + y + z = 1     →           x + y = 1         →

y = 1 - x

Logo, o y varia de 0 até essa reta...

0 ≤ y ≤ 1 - x

Enquanto x , varia no intervalo numérico de 0 até 1 ...

0 ≤ x ≤ 1

Para definirmos os limites de z , repare mais uma vez no sólido, mas dessa vez prestando atenção onde z varia...

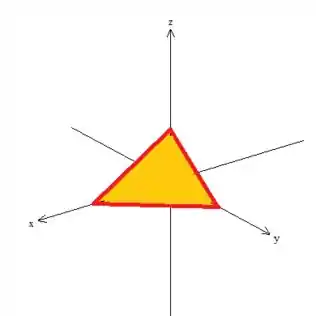
Veja que z entra lá em baixo no plano z = 0 e sai no plano laranja...

0 ≤ z ≤ p l a n o   l a r a n j a

Como o plano azul é x + y + z = 1 ...

0 ≤ z ≤ 1 - x - y

Logo, a integral tripla fica sendo...

4 ∭ W   d V = 4 ∫ 0 1 ∫ 0 1 - x ∫ 0 1 - x - y d z d y d x

Agora é só resolve-la!

Passo 5

Calculando a integral de dentro...

4 ∫ 0 1 ∫ 0 1 - x ∫ 0 1 - x - y d z d y d x = 4 ∫ 0 1 ∫ 0 1 - x 1 - x - y d y d x =

Calculando a do meio...

4 ∫ 0 1 ∫ 0 1 - x 1 - x - y d y d x = 4 ∫ 0 1 y - x y - y 2 2 0 1 - x d x =

4 ∫ 0 1 1 - x - x 1 - x - 1 - x 2 2 d x =

4 ∫ 0 1 1 - 2 x + x 2 - 1 - 2 x + x 2 2 d x = 4 ∫ 0 1 1 2 - x + 1 2 x 2 d x =

4 1 2 x - x 2 2 + x 3 6 0 1 = 4 1 2 - 1 2 + 1 6 =

2 3

Bem, esse é o resultado da integral de superfície que estávamos afim ;)

∬ S   F → ⋅ d S → = 2 3

Resposta

2 3

Exercícios de Livros Relacionados

Nos Exercícios 1-4, encontre a divergência do campo.4. O campo de velocidade da Figura 16.13.
Nos Exercícios 1-4, encontre a divergência do campo.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
(Divergente em coordenadas polares) Seja Ω um campo aberto no semiplano y0 e seja F → x , y = P x , y i → + Q x , y j → , x , y ∈ Ω , com PeQ de classe C 1 . Seja P 1 θ ,ρ = P x , y e Q 1 θ ,ρ = Q x ,