Calcule , onde e é formada pelas faces (exceto pelo fundo) do tetraedro de vértices , , e .
Passo 1
Oiiie, tudo bem com você?
O enunciado nos pede para calcularmos o fluxo , nos dando o campo vetorial
e a superfície é dada pelo tetraedro de vértices , , e . Para calcular o fluxo devemos resolver a seguinte integração
Aqui em cima temos um campo vetorial complicado e uma superfície bastante simples! Isso é comum em problemas que usam o teorema de Gauss, que nos diz
Maravilha! Vamos tentar aplicar isso! Vem comigo!
Passo 2
Antes de qualquer coisa, vamos calcular a divergência do nosso campo! Temos que o operador é definido como
em que temos . Identificando que , temos que a primeira derivada parcial é
já que derivadas parciais consideram tudo que não é a variável desejada como constante! Analogamente, temos que a segunda derivada é
e, por último, temos que
Portanto, temos que a divergência é tal que
e, a integral se torna
Ótimo! Só precisamos ver quais são os limites de integração delimitados por nosso tetraedro!
Passo 3
O nosso tetraedro é o seguinte
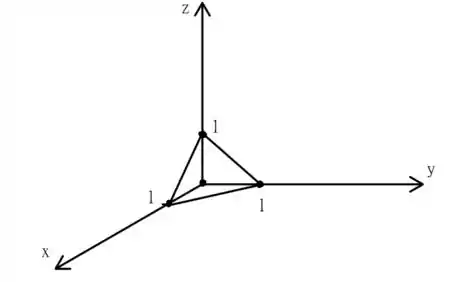
Vamos ter que determinar limites de integração para cada variável, . O primeiro é o mais simples, podemos escolher começar pelo eixo , e dizer que ele tem obedece o seguinte intervalo
Faz sentido, certo? Agora os outros são um pouco mais chatos! Note que a partir de um ponto qualquer no intervalo acima, temos que o valor de , varia no intervalo
Precisamos achar essa reta!!! Vamos fazer isso!
Passo 4
A reta no plano , passa pelos seguintes pontos e , portanto, podemos usar a seguinte definição para a equação da reta
em que é qualquer ponto que a reta cruze! O coeficiente angular é dado por
ou seja, temos que , e a equação da reta é dada por
em que escolhi , simplificando, temos que
Os limites de são dados então por
Ainda faltam os limites de ! Vamos lá!
Passo 5
Agora, se pegarmos um ponto de coordenadas qualquer no plano e subirmos, iremos ver que os limites de são dados por
Para achar esse plano precisamos lembrar a equação geral do plano como
em que é um vetor normal ao plano, e é obtido conhecendo um ponto que pertence ao plano! Como podemos obter o vetor normal? Fazendo o produto vetorial entre dois vetores que pertencem ao plano, como conhecemos três pontos pertencentes ao plano, podemos construir os dois vetores necessários! Consegue visualizar? Vem comigo!
Passo 6
Podemos definir um vetor como
e, também
Usando os vértices como os pontos
, e
Temos que nossos dois vetores serão
e, também
usando a definição de produto vetorial, temos que
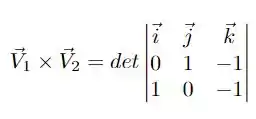
ou seja, nosso vetor normal é
Maravilha! Vamos escrever a equação do plano!
Passo 7
Lembrando a equação geral do plano e usando nosso vetor normal, temos que
Portanto, temos que
podemos usar qualquer vértice para achar , usando que , temos
nos dá , e a equação do plano será
E, portanto, os limites de integração em são
Finalmente! Vamos resolver nossa integral!
Passo 8
Usando os limites de integração temos que
A integral mais interna nos dá
Portanto
Vamos resolver agora as integrais em , temos que
ou, usando a regrinha para identificar primitivas de polinômios, temos
e, por último, temos
Uff… Respira um pouco! E, vamos agora resolver as integrais em Saca só!
Passo 9
Somando os três resultados anteriores, temos que
juntando tudo em uma só integral, temos que
usando novamente a regrinha do polinômio para integrais, temos que
ou, simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!