Calcule , onde está orientada pela normal exterior nos seguintes casos:
é a fronteira da região limitada por e .
Passo 1
Eaew, belezinha?
Precisamos calcular a integral de superfície
Essa notação com produto exterior pode ser um pouco assustadora, então vamos considerar o seguinte formato equivalente
temos que a nossa superfície vai ser a região limitada por
e
Para resolver isso, vamos usar o teorema da divergência de Gauss, já que o campo vetorial é meio chatinho! Temos que o teorema diz
Muitas vezes é mais simples resolver a integral tripla do que calcular explicitamente a integral de superfície! Vamos lá!
Passo 2
Vamos calcular de cara a divergência do campo vetorial, temos por definição que
em que
calculando as derivadas parciais e somando todos os termos, obtemos que a divergência tem a seguinte forma
bem mais simples não é? A nossa integral se torna então
Mas, e qual é a nossa região? Vamos trabalhar com ela um pouco!
Passo 3
O sólido pode ser representado pela seguinte figura
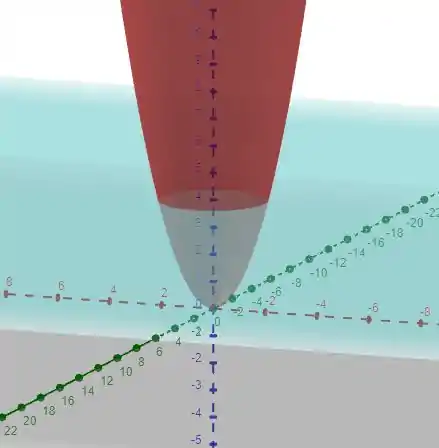
que é um parabolóide cortado por um plano! Desta forma, o mais conveniente é escrever tudo em coordenadas cilíndricas dadas por
, e
lembrando que em coordenadas cilíndricas temos . Note que , uma vez que a intersecção do plano com o parabolóide nos leva a circunferência
temos também que , que , note pelo desenho que a variável parte do parabolóide ao plano! Parece tudo simples até aí! Mas é preciso lembrar que o teorema de Gauss vale para superfícies fechadas, então, precisamos considerar as integrais de superfície através da tampa em e pelo parabolóide, de forma que nossa integral se torna
Note que ainda não mudei as coordenadas pois será conveniente integrar em antes de realizar a mudança! Vamos lá!
Passo 4
Integrar em primeiro é uma necessidade já que os limites dependem das outras variáveis, temos então que
Integrando usando a regrinha do polinômio para integrais, temos que
Avaliando os limites, temos então que
Agora sim! Podemos mudar para coordenadas polares! Bora lá!
Passo 5
Fazendo a mudança para coordenadas polares temos a conveniência de que , portanto, obtemos
Começando pela integral em , temos que
Expandindo usando a relação de meio ângulo para o seno
usando as integrais conhecidas para o seno e cosseno, temos que
Avaliando os limites obtemos simplesmente
Falta apenas a integral em ! Bora lá!
Passo 6
Distribuindo nas integrais que restaram, obtemos
Usando a regrinha do polinômio para integrais, temos que
Avaliando os limites de integração
A questão foi isso! Te vejo na próxima! Tchau Tchau!