Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Gauss

Ver Teoria
Exercício 52123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051535455565758596061626364656667686970717273747576777879808182

Enunciado

USP, Sem Campus, Cálculo 3, lista 3 - 2021.1, Questão 19c

Calcule o fluxo F → através de S ( N → = normal unitária exterior), para:

( c ) F → ( x , y , z ) = x i → + y j → + z k → ( x 2 + y 2 + z 2 ) 3 + z k → e S = { ( x , y , z ) ∈ R 3 : x 2 + y 2 = ( z - 2 ) 2 , 0 ≤ z ≤ 2 } sendo N → o campo de vetores unitários normais a S tal que N → ⋅ k → > 0 .

Passo 1

Eaew, belezinha?

Precisamos calcular o fluxo do seguinte campo vetorial

F → ( x , y , z ) = x i → + y j → + z k → ( x 2 + y 2 + z 2 ) 3 + z k →

através da superfície S limitada pelos hemisférios

S = { ( x , y , z ) ∈ R 3 : x 2 + y 2 = ( z - 2 ) 2 , 0 ≤ z ≤ 2 }

O cálculo de fluxos pode ser feito através da seguinte expressão

∫ ∫ S F → ⋅ n →   d S = ∫ ∫ ∫ V d i v ( F → )   d V

Acima temos o teorema de Gauss, descobrir se é interessante expandir o lado esquerdo ou o lado direito da expressão acima é caminho! Bora lá!

Passo 2

Vamos calcular a divergência do campo vetorial, nós temos que

d i v ( F → ) = ∂ F x ∂ x + ∂ F y ∂ y + ∂ F z ∂ z

em que F → ( x , y , z ) = ( F x , F y , F z ) = ( x ( x 2 + y 2 + z 2 ) 3 , y ( x 2 + y 2 + z 2 ) 3 , z ( x 2 + y 2 + z 2 ) 3 + z ) . Usando a regra do quociente e evidenciando termos em comum, você pode escrever que

∂ F x ∂ x   = - 2 x 2 + y 2 + z 2 ( x 2 + y 2 + z 2 ) 5 / 2

e, analogamente, você conseguirá mostrar que

∂ F y ∂ y   = - 2 y 2 + x 2 + z 2 ( x 2 + y 2 + z 2 ) 5 / 2 e ∂ F z ∂ z   = - 2 z 2 + x 2 + y 2 ( x 2 + y 2 + z 2 ) 5 / 2 + 1

A soma dos três componentes miraculosamente resulta em

d i v ( F → ) = - 2 x 2 + y 2 + z 2 ( x 2 + y 2 + z 2 ) 5 / 2 + - 2 y 2 + x 2 + z 2 ( x 2 + y 2 + z 2 ) 5 / 2 + - 2 z 2 + x 2 + y 2 ( x 2 + y 2 + z 2 ) 5 / 2 + 1 = 1

Ficou até bastante simples! Talvez seja conveniente expandir a nossa integral tripla! Mas, antes disso, vamos dar uma olhada em nossa região, ela é a seguinte

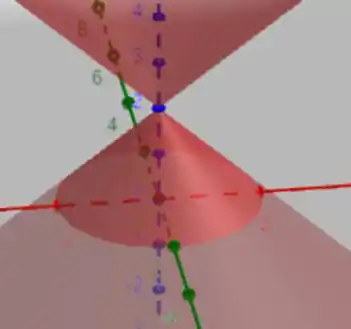
Ou seja, queremos tudo que está acima de z = 0 e abaixo de z = 2 no cone acima! Para um cone costuma ser conveniente utilizar coordenadas cilíndricas! Bora lá!

Passo 3

Vamos escrever nosso cone usando a seguinte mudança de coordenada

x = r   c o s ( θ ) , y = r   s e n ( θ ) e z = z

e, o jacobiano já conhecido como

J = r

de forma que a nossa integral se torna

∫ ∫ S F → ⋅ n →   d S = ∫ ∫ ∫ V ( 1 ) r   d r   d θ   d z

Vamos analisar os limites de integração! Note que o raio é o raio da circunferência em que o cone intercepta z = 0 , portanto, 0 ≤ r ≤ 2 , temos que a circunferência é completa, portanto 0 ≤ θ ≤ 2 π , e o que precisamos tomar mais cuidado é a altura z , que vai do plano z = 0 até o cone z = - x 2 + y 2 + 2 = 2 - r , note que escolhi o valor negativo para a raiz pois é a parte inferior do cone que estamos considerando! A nossa integral se torna

∫ ∫ S F → ⋅ n →   d S = ∫ 0 2 π ∫ 0 2 ∫ 0 2 - r r   d z   d r   d θ

Vamos começar com a integração em z ! Vem comigo!

Passo 4

Precisamos integrar primeiro em z uma vez que seus limites não são constantes, temos que

∫ ∫ S F → ⋅ n →   d S = ∫ 0 2 π ∫ 0 2 r   d r   d θ ∫ 0 2 - r   d z

Essa integração é bastante direta, podemos identificar que

∫ 0 2 - r   d z = z | 0 2 - r = 2 - r

Nos restando para resolver a integração

∫ ∫ S F → ⋅ n →   d S = ∫ 0 2 π ∫ 0 2 r ( 2 - r ) d r   d θ = 2 ∫ 0 2 π ∫ 0 2 r d r   d θ - ∫ 0 2 π ∫ 0 2 r 2 d r   d θ

usando a regrinha do polinômio para as integrais em r , temos que

∫ ∫ S F → ⋅ n →   d S = 2 ∫ 0 2 π 1 2 [ r 2 ] | 0 2   d θ - ∫ 0 2 π 1 3 [ r 3 ] | 0 2   d θ = 4 ∫ 0 2 π d θ - 8 3 ∫ 0 2 π d θ

A integral em θ pode ser identificada diretamente como

∫ ∫ S F → ⋅ n →   d S = 4 [ θ ] | 0 2 π - 8 3 [ θ ] | 0 2 π = 8 π - 16 π 3

ou simplesmente

∫ ∫ S F → ⋅ n →   d S = 8 π 3

Note que se você quisesse, poderia ter encontrado o mesmo resultado usando que

V c o n e = A r e a b a s e × A l t u r a 3

A questão é isso! Te vejo na próxima! Tchau Tchau!

Resposta

∫ ∫ S F → ⋅ n →   d S = 8 π 3

Exercícios de Livros Relacionados

Nos Exercícios 1-4, encontre a divergência do campo.4. O campo de velocidade da Figura 16.13.
Nos Exercícios 1-4, encontre a divergência do campo.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
(Divergente em coordenadas polares) Seja Ω um campo aberto no semiplano y0 e seja F → x , y = P x , y i → + Q x , y j → , x , y ∈ Ω , com PeQ de classe C 1 . Seja P 1 θ ,ρ = P x , y e Q 1 θ ,ρ = Q x ,