Calcule as seguintes integrais
, onde e é a parte de com , orientada com a normal unitária ;
Passo 1
Oiie, tudo bem com você?
Temos que calcular a seguinte integral de superfície
em que o campo vetorial considerado é dado por
Existe uma identificação bastante direta, através do teorema da divergência de Gauss que pode ser útil, temos que
mas note que no lado esquerdo temos uma superfície que é fronteira do sólido . Para sabermos qual identificação vale a pena trabalhar, precisamos verificar a nossa superfície! Saca só!
Passo 2
A nossas região pode ser visualizada como
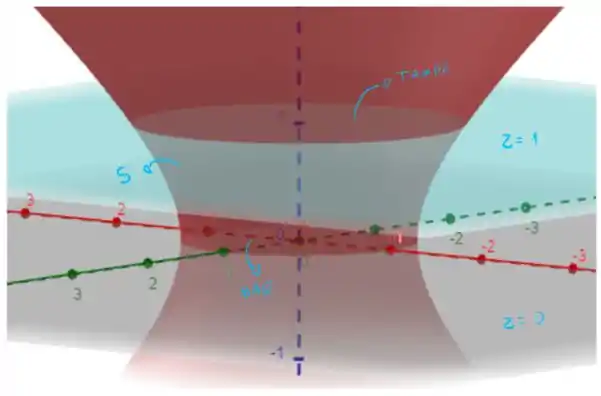
A nossa superfície é a lateral de um sólido , que tem como base e tampa dois planos. Então, podemos considerar o teorema da divergência de Gauss, usando um da forma
que é fronteira de , e portanto, a nossa integral pode ser identificada como
A integral que nós queremos é apenas uma parte do lado esquerdo do teorema de Gauss, portanto, vamos ter que calcular as outras três componentes. No entanto, isso é um pouco mais fácil do que expandir a integral de superfície normalmente! Saca só!
Passo 3
Vamos começar calculando o lado direito, temos que a divergência do campo é tal que
em que . Substituindo então o campo dado no enunciado, temos que
Aplicando a regra do quociente junto com a regra da cadeia, e lembrando que em derivadas parciais toda variável que não é derivada é tomada como constante, obtemos que
evidenciando o denominador, e o termo , temos que
Portanto, temos que
Precisamos então resolver a seguinte integração
Vamos obter os nossos limites de integração! Saca só!
Passo 4
O sólido tem simetria cilíndrica, portanto, usando coordenadas cilíndricas, obtemos que
, e
de forma que . Temos que os limites de integração são dados por , pois o sólido tem uma completa revolução no ângulo polar. A coordenada radial pode ser obtida fazendo a intersecção entre o cilindro e o hiperbolóide
uma vez que temos que , note que podemos obter
desta forma temos os limites . E, por último, temos que a coordenada vai do plano até . Temos que resolver então
Vamos precisar resolver a integral em primeiro pois temos que seus limites são da forma . Vamos lá!
Passo 5
A integral em é tal que
de forma que a nossa integral se reduz à
A integral em é obtida analogamente como
nos restando apenas
A última integral é simplesmente
Portanto, temos que
Maravilha! Mas, ainda precisamos resolver o lado esquerdo de nosso teorema para a base e a tampa! Então! Vamos lá!
Passo 6
O nosso problema está resumido em
Vamos analisar as duas integrais em conjunto, primeiro, discutindo quem são os vetores normais! Pela nossa figura, e levando em consideração que a normal considerada para a nossa superfície é tal que (ou seja, o vetor normal externo a superfície ), temos que a tampa tem um vetor normal dado por
e, a base, analogamente, tem vetor normal
Usando o formato de nosso campo vetorial, e resolvendo os produtos escalares nas integrais de superfície, temos que
como temos que a base está em e a tampa em , isso se resume à
Vamos tentar obter uma região que descreva a nossa superfície! Vem comigo!
Passo 7
Se usarmos coordenadas polares temos que e , e , obtemos então que
temos que a superfície é delimitada pela circunferência.
portanto, . Portanto, temos que
usando que . E, que a revolução é completa, temos que
Maravilha! Vamos cuidar de resolver essa integral que falta agora! Bora lá!
Passo 8
Temos que resolver a seguinte integração
Para a primeira integral em , é conveniente fazer a substituição simples
e
de forma que a integral se torna
como temos que e , a nossa integral pode ser obtida como
Avaliando os limites, temos que
A segunda integral em é um pouco mais direta, temos que
Vamos voltar estes resultados para o nosso problema! Saca só!
Passo 9
Usando os resultados que obtivemos no passo anterior, temos que
como temos que
Obtemos que
Juntando então todos os nossos resultados, temos que
Portanto, a integral que desejamos é tal que
Tirando em evidência, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!