Calcule , onde , é a superfície cilíndrica fechada limitada pelos planos e , cuja base no plano é limitada pelas curvas de equações:
E o vetor normal é exterior à .
Passo 1
Pelo aspecto do campo vetorial, ficamos inclinados à aplicar o Teorema de Gauss:
Calculando o divergente:
Passo 2
Agora precisamos determinar os limites de integração em . Fazendo o desenho do cilindro, que não é tão difícil pois são vários semicírculos, obtemos:
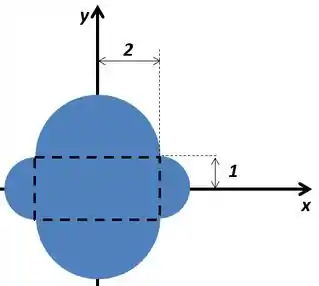
Aplicando a fórmula, temos simplesmente o dobro do volume da região:
Que é constituída basicamente de uma circunferência de raio , uma de raio e um retângulo de lados e . A altura é .
Substituindo:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 1-4, encontre a divergência do campo.4. O campo de velocidade da Figura 16.13.
Nos Exercícios 1-4, encontre a divergência do campo.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
(Divergente em coordenadas polares) Seja Ω um campo aberto no semiplano y0 e seja F → x , y = P x , y i → + Q x , y j → , x , y ∈ Ω , com PeQ de classe C 1 . Seja P 1 θ ,ρ = P x , y e Q 1 θ ,ρ = Q x ,