Questão 3:
Calcule
onde
e , sendo a parte do paraboloide , , orientada de modo que sua normal unitária satisfaça e a parte do paraboloide , orientada de modo que sua normal unitária satisfaça .
Passo 1
Bem, acho que você já percebeu que essa integral de superfície não será feita de uma forma direta, afinal o campo é horroroso e a superfície também, mesmo sem desenha-la, é bem feia por definição.
O segredo aqui então é tentar usar o Teorema de Gauss. Para você ter certeza, busquemos o divergente ;)
Como...
Calculando as derivadas parciais tomando o devido cuidado...
Com um divergente desses, certamente é Gauss !
Passo 2
Pelo Teorema de Gauss...
Agora, não podemos sair aplicando essa linda igualdade assim, neh? Temos que antes averiguar as condições do Teorema:
1º - Precisamos de uma superfície fechada delimitando um sólido .
2º - O Campo não pode ter singularidades no sólido e nem na superfície.
3º - Além disso, temos que ter uma superfície-sólido orientado positivamente.
Passo 3
O primeiro se refere à superfície que deve ser fechada delimitando um sólido no seu interior. Agora, será que isso está acontecendo? Para averiguar a resposta, desenhemos a superfície :
O problema nos disse que é uma superfície união de outras duas: e , onde é um paraboloide com a boca pra baixo, passando por e é um paraboloide com a boca pra cima passando por ...
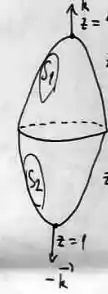
Não esquenta na hora de desenhar esses caras com a perfeição, pois só queremos um esboço mesmo, ok?
Bem, a superfície é fechada, e delimita um cara fechado dentro dele ;)
Passo 4
A outra condição nos pede um campo sem singularidades onde estamos trabalhando, e olha que legal
O campo não tem singularidades (divisão por zero ou coisa parecida) em lugar algum!
Passo 5
A última condição, nos fala que precisamos de uma superfície orientada positivamente, o que significa que o vetor normal deve estar saindo do sólido. Se você observar o enunciado, ele fala que no ponto em , o vetor é pra cima
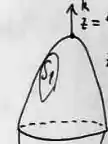
E em , no ponto o vetor é...
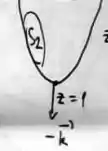
Ou seja, de fato o sólido está orientado positivamente.
Passo 6
Com as condições ok, podemos aplicar a igualdade de Gauss para matarmos o problema:
No caso trocamos o problema de calcular a integral de superfície por um problema de calcular a integral tripla:
Para isso, precisamos do sólido descrito. Como está dentro de dois paraboloides, podemos descrevê-lo em coordenadas cilíndricas, observe!
Passo 7
Para descobrirmos que cilindro estamos trabalhando, devemos encontrar a intersecção entre esses dois paraboloides.
Observe que essa intersecção acontece justamente no (coordenada que ambos têm em comum). Substituindo na equação de um deles...
Então o cilindro que contêm o sólido é um de base elíptica, e a mudança de coordenadas que devemos fazer então é...
Não se esqueça do Jacobiano, que no caso de uma mudança para coordenadas elípticas vale...
O raio está variando de a e dá uma volta completa...
Quanto ao , bem ele entra no sólido no paraboloide baixo e sai no de cima...
Como o paraboloide de cima é e o de baixo é ...
Em coordenadas cilíndricas...
Como ...
Passo 8
Substituindo então esses dados na integral tripla...
Integrando em considerando toda a exressão que não tem como constante...
Simplificando mais um pouco...
Agora calculando a integral do meio...
Por fim...