Um potenciômetro (dimmer) é um dispositivo que permite variar a intensidade luminosa de uma lâmpada. Estes dispositivos são compostos por uma bobina de indutância variável em série com uma lâmpada(Figura ).
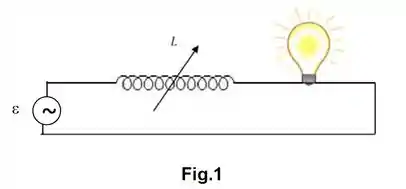
O circuito é alimentado por um gerador alternado com uma eficaz e uma frequência angular . Considere que a lâmpada utilizada é de de potência e que a sua resistência elétrica seja independente da temperatura.
Calcule qual deve ser o valor mínimo da indutância para que a potencia média dissipada na lâmpada seja máxima .
Calcule qual deve ser o valor máximo da indutância para que a potencia média dissipada pela lâmpada seja .
Se no lugar do gerador de alternada fosse inserida uma bateria em corrente continua , qual deveria ser o valor da tensão para que, decorrido um tempo muito longo, a potência dissipada na lâmpada fosse de ?
Considere novamente o circuito da Figura . Agora a lâmpada é substituída por um resistor do mesmo valor e no circuito é inserido em série um capacitor .
Considerando que a indutância possui o valor máximo calculado no item desenhe o diagrama de fasores do circuito. A corrente que passa no circuito está adiantada ou atrasada em relação à tensão do gerador?
Mudando o valor da indutância entre os limites calculados nos itens e é possível fazer com que o circuito entre em ressonância? Em caso de resposta negativa justifique. Em caso de resposta afirmativa calcule o valor de para que isso aconteça.
Passo 1
Para um circuito RLC, temos que a potência dissipada é dada pela seguinte fórmula:
Onde e , lembrando que . Substituindo:
Para que , como o valor de e não variam, a única maneira de ter a potência máxima é quando for mínimo, ou seja, , nesse caso, .
Passo 2
Para , usando a relação anterior, temos:
Substituindo e os outros valores, temos:
Passo 3
Para um tempo muito longo, temos que o indutor irá se comportar como um fio normal, sem resistência, logo, a potencia dissipada será:
Passo 4
Agora, temos um novo circuito, onde , além disso, temos um novo componente, o capacitor, para esse circuito, vamos determinar as reatâncias:
Logo, o diagrama pode ser representado da seguinte forma:
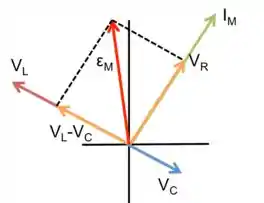
Logo, a corrente está atrasada em relação à tensão!
Passo 5
Para que o circuot0 entre em ressonância, precisamos que:
Substituindo os valores, temos:
Portanto , existe sim um valor de , entre e para que o circuito entre em ressonância!
Resposta
Ver figura. Corrente atrasada em relação à tensão.