. Considere um circuito em série que tem uma capacitância e uma indutância . No momento inicial, , o capacitor possui carga nula, mas está sendo carregado por uma corrente .
Supondo uma solução do tipo , encontre , e .
Qual é o período de oscilação deste sistema.
Obtenha e esboce um gráfico das funções das energias elétrica (, no capacitor) e magnética (, no indutor), em função do tempo. Indique claramente os seus valores máximos e a escala de tempo.
Se colocarmos uma fonte de tensão alternada forçando este sistema, dada por , para qual valor de a corrente do circuito será máxima.
Passo 1
Vem comigo que vamos detonar essa questão!
Para não ter confusão vou explicar e resolver cada item separadamente em cada passo. Já que a questão é meio grande e pede bastante coisa.
Passo 2
Vamos começar com o item .
Ele quer que encontremos os parâmetros (frequência angular), (carga máxima) e (fase).
Primeiro vamos encontrar .
A frequência angular de um circuito é dada por:
Substituindo como que temos, ficamos com:
Passo 3
Agora vamos encontrar .
O enunciado nos deu como a carga se comporta com o tempo.
Se derivarmos isso em função do tempo teremos como a corrente se comporta em função do tempo, assim temos:
Onde a amplitude dessa corrente é , logo temos que:
O enunciado nos fornece essa corrente máxima, que vai ser , assim temos que:
Passo 4
Agora falta achar para completar o item . Para isso vamos usar as condições iniciais do problema, segundo o enunciado em , temos:
Para que isso ocorra simultaneamente, temos que:
Pronto, terminamos o item .
Passo 5
Agora vamos resolver .
Ele quer o período de oscilação do sistema. Para encontrar isso vamos usar o fato de que:
Usando o valor que temos para , ficamos com:
Fechou o item
Passo 6
Agora temos o item .
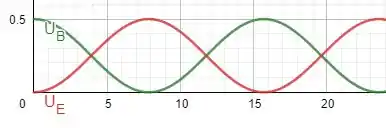
Ele quer que encontremos expressões para energia no capacitor e no indutor e esbocemos o gráfico dessas energias.
Temos que a energia em um capacitor é dada por:
Usando que , logo temos:
A energia em um indutor é dada por:
Usando que , logo temos:
Com isso temos o seguinte gráfico:
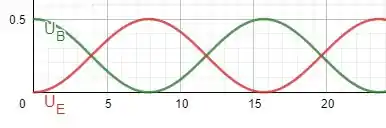
O gráfico está em .
Passo 7
E finalmente o item .
Ele quer saber o valor de onde teremos corrente máxima, para uma fonte alternada .
Mas para que tenhamos corrente máxima o circuito tem que estar em ressonância e isso ocorre quando as frequências de oscilação do circuito e da fonte são iguais, logo:
E finalmente terminamos esse problema.
Resposta