(a)
(b)
(c)
(d)
(e)
(a)
(b)
(c)
(d)
(e)
Passo 1
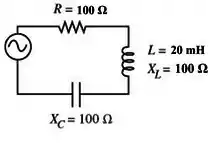
18a) Calcular a frequência de oscilação da fonte, olhando para o indutor:
Passo 2
Com essa frequência, aplicar na equação da impedância capacitiva:
Passo 3
18b) A corrente eficaz multiplicada pela reatância total é igual é igual ao valor eficaz da fonte.
Passo 4
Notar que o circuito está em ressonância: a reatância do indutor é igual à do capacitor.
Passo 5
Por isso, podemos imaginar que as reatâncias do indutor e do capacitor se cancelam e sobra só o resistor:
Resposta
18a) (d)
18b) (b)
Exercícios de Livros Relacionados
Na Fig. 31-37, um gerador trifásico G produz energia elétrica que é transmitida através de três fios. Os potenciais dos três fios (em relação a uma referência comum) são V 1 = As e nω t para o fio 1,
Que corrente contínua produz a mesma energia térmica, em um certo resistor, que uma corrente alternada com um valor máximo de 2,60A ?
A figura 31-35 mostra um gerador de CA ligado aos terminais de uma “caixa-preta”. A caixa contém um circuito R L C , possivelmente com mais de uma malha, cujos elementos e ligações são desconhecidos.
Um dimmer típico, com os que são usados para regular a luminosidade das lâmpadas do palco nos teatros, é composto por um indutor variável L (cuja indutância pode ser ajustada entre zero e L m a x ) li
Um gerador de CA alimenta uam carga resistiva em uma fábrica distante através de uma linha de transmissão de dois cabos. Na fábrica, um transformador abaixador de tensão reduz a tensão do valor de tra