UFF - Física 3 - P3 2017.1 - 12
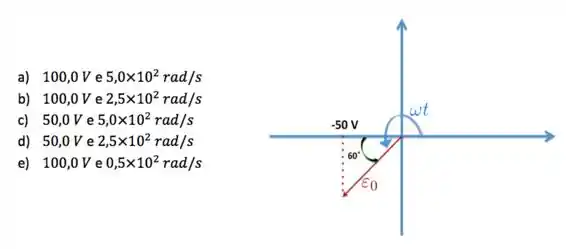
Considere que o diagrama abaixo descreva a voltagem de uma fonte CA no instante . Os valores de pico da fem e da frequência angular da fonte CA são, respectivamente,
Passo 1
Nessa questão, temos uma fem oscilante no tempo, cujo valor máximo é dado por , como mostra a figura acima. Usando um pouco de geometria, a gente percebe é fácil encontrar o valor que o fasor faz com o eixo horizontal:
Passo 2
No enunciado do problema, temos que . Substituindo na expressão acima para , obtemos:
Passo 3
Para obter , dá uma olhada na figura e repare no triângulo retângulo formado pelo fasor e a linha tracejada. Como temos o valor do cateto adjacente ao ângulo , então podemos utilizar a seguinte trigonométrica:
o que dá .
Resposta
Portanto, e , letra a).
Exercícios de Livros Relacionados
Na Fig. 31-37, um gerador trifásico G produz energia elétrica que é transmitida através de três fios. Os potenciais dos três fios (em relação a uma referência comum) são V 1 = As e nω t para o fio 1,
Que corrente contínua produz a mesma energia térmica, em um certo resistor, que uma corrente alternada com um valor máximo de 2,60A ?
A figura 31-35 mostra um gerador de CA ligado aos terminais de uma “caixa-preta”. A caixa contém um circuito R L C , possivelmente com mais de uma malha, cujos elementos e ligações são desconhecidos.
Um dimmer típico, com os que são usados para regular a luminosidade das lâmpadas do palco nos teatros, é composto por um indutor variável L (cuja indutância pode ser ajustada entre zero e L m a x ) li
Um gerador de CA alimenta uam carga resistiva em uma fábrica distante através de uma linha de transmissão de dois cabos. Na fábrica, um transformador abaixador de tensão reduz a tensão do valor de tra