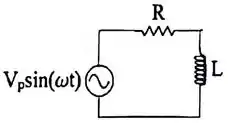
Se a frequência no circuito da figura aumentar, mantendo a amplitude da fonte constante, a corrente através do resistor
- Aumentará
- Diminuirá
- Não se altera
- Poderá aumentar ou diminuir, dependendo do valor original da frequência
- Poderá aumentar ou diminuir, dependendo dos valores de e de
Passo 1
Aqui aplicamos diretamente a lei das malhas
Supondo que a corrente seja dada por
De forma que
Substituindo na nossa EDO
Podemos resolver essa equação por fasores!
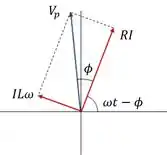
O fasor do lado esquerdo é igual a soma dos fasores do lado direito, e como eles são perpendiculares entre si, podemos usar o teorema de Pitagorás .
Para esta equação para a amplitude da corrente, vemos que ao aumentar a frequência diminuímos a amplitude da corrente.
Resposta
(b)
Exercícios de Livros Relacionados
Na Fig. 31-37, um gerador trifásico G produz energia elétrica que é transmitida através de três fios. Os potenciais dos três fios (em relação a uma referência comum) são V 1 = As e nω t para o fio 1,
Que corrente contínua produz a mesma energia térmica, em um certo resistor, que uma corrente alternada com um valor máximo de 2,60A ?
A figura 31-35 mostra um gerador de CA ligado aos terminais de uma “caixa-preta”. A caixa contém um circuito R L C , possivelmente com mais de uma malha, cujos elementos e ligações são desconhecidos.
Um dimmer típico, com os que são usados para regular a luminosidade das lâmpadas do palco nos teatros, é composto por um indutor variável L (cuja indutância pode ser ajustada entre zero e L m a x ) li
Um gerador de CA alimenta uam carga resistiva em uma fábrica distante através de uma linha de transmissão de dois cabos. Na fábrica, um transformador abaixador de tensão reduz a tensão do valor de tra