Um gerador de de frequência angular alimenta um dispositivo em sérei com um capacitor de . No dispositivo a voltagem está adiantada de radianos em relação à corrente no circuito. A tensão no gerador cujo valor eficaz é de está em fase com a corrente. A corrente no circuito é de .
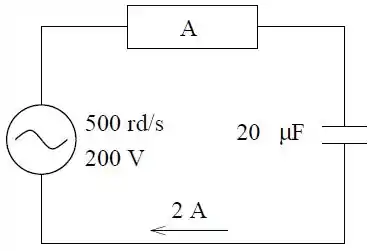
- Determine a potência média fornecida pelo gerador e a tensão eficaz no capacitor;
- Faça um diagrama indicando claramente os Fasores das tensões e da corrente. Determine a tensão eficaz no dispositivo e a sua defasagem em relação à corrente;
- Escreva a expressão da tensão no capacitor em função do tempo (adote fase inicial nula para a corrente);
Dado: .
Passo 1
- Determine a potência média fornecida pelo gerador e a tensão eficaz no capacitor;
- Faça um diagrama indicando claramente os Fasores das tensões e da corrente. Determine a tensão eficaz no dispositivo e a sua defasagem em relação à corrente;
- Escreva a expressão da tensão no capacitor em função do tempo (adote fase inicial nula para a corrente);
Bom... o problema já nos disse que e . Logo:
A tensão eficaz no capacitor é dada por:
Onde e . Logo:
O que faz bastante sentido... já que o circuito é composto somente do capacitor e da fonte, a tensão eficaz no capacitor será justamente a tensão na fonte.
Passo 2
A tensão eficaz no dispositivo é dada por:
A defasagem é dada por:
Um último detalhe que você precisa lembrar é que a tensão capacitiva está sempre atrasada em relação à tensão da fonte.
Logo, o diagrama vai ficar dessa forma:
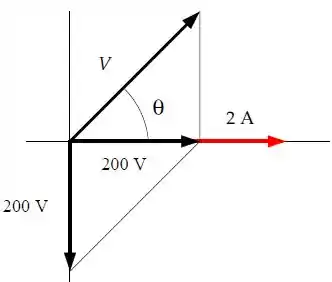
Passo 3
Como a corrente que passa pelo circuito é alternada, a tensão no capacitor vai ser essa cara:
Portanto:
Resposta
a.
b.
c.